Cho tam giác ABC có AB=AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm K sao cho AD=AK.
a) Chứng minh: DC=BK
b) Điểm E là giao điểm của DC và BK. Chứng minh tam giác EDB= tam giác EKC
Những câu hỏi liên quan
Cho tam giác ABC, trên tia đối AB lấy điểm D sao cho AB=AD. Trên cạnh AC lấy điểm G sao cho AG =1/3 AC. Gọi E là giao điểm BG và DC. Chứng minh E Là trung điểm DC
Cho tam giác ABC có AB<AC trên cạnh AC lấy điểm D sai cho AD=AB gọi M là trung điểm của đoạn thẳng BD
a) Chứng minh tam giác ABM = tam giác ADM
b) Tia AM cắt cạnh BC taị K chứng minh tam giác ABK và tam giác ADK
c) trên tia đối của tia BA lấy điểm E Sao cho BE=DC chứng minh 3 điểm E,KD thẳng hàng
Tự vẽ hình được nha bạn ^^.
a, Vì M là trung điểm của đoạn thẳng BD
=> MB = MD = BD: 2
Xét tam giác ADM và tam giác ABM:
AM: Cạnh chung
AB = AD
MB = MD ( chứng minh trên )
Do đó: \(\Delta ABM=\Delta ADM\left(c.c.c\right)\)
Phần b sai đề, vì phần c có liên quan đến phần b mà phần b sai đề => phần c cũng sai đề
Đúng 0
Bình luận (2)
Cho tam giác ABC có AB<AC trên cạnh AC lấy điểm D sao cho AD = AB gọi M là trung điểm của đoạn BD:
a) TM cắt cạnh BC tại K.Chứng minh tam giác ABK=tam giác ADK
b)Trên tia đối của tia BA lấy điểm E sao cho BE=DC Chứng minh rằng ba điểm E,K,D thẳng hàng
Xét 2 tam giác ABM và ADM có
AB = AD
BM = DM => tam giác ABM = tam giác ADM (c.c.c)
Cạnh AM chung
=> A1 = A2
B1 = D1
M1 = M2
Vì M1 kề bù với M2
=> M1 + M2 = 180
=>2 M1 = 180
=> M1 = 90
=< M2 = 90
Vì M1 kề bù vs M4
M2 kề bù vs M3
=> M1 + M4 = M2 + M3 = 180
Mà M1 = M2 = 90
=> M4 = 180 - 90 = 90
M3 = 180 - 90 = 90
=> M3 = M4
Xét 2 tam giác KMD và KMB có :
M3 = M4
BM = DM => tam giác KMD = tam giác KMB (c.g.c)
MK là cạnh chung
=> BK = DK
Xét 2 tam giác ABK và ADK có :
AB = AD
BK = DK => tam giác ABK = ADK (c.c.c)
AK là cạnh chung
b) Đợi tý , tớ suy nghĩ đã
Đúng 0
Bình luận (1)
theo tớ , đề câu a phải là :
AM cắt cạnh BC tại K.Chứng minh tam giác ABK=tam giác ADK
Đúng 0
Bình luận (2)
Câu b tớ nghĩ ko ra , nhờ soyeon_Tiểubàng giải ấy , chỉ cần chứng minh Góc AKE +
góc AKD = 180 là được .
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
Cho tam giác ABC có AB = AC . Trên 2 cạnh AB , AC lần lượt là lấy 2 điểm D , E sao cho
AD = AE
Chưng minh rằng
a, BE = DC
B , Gọi F là giao điểm của ED và DC . Chứng minh FD = FE
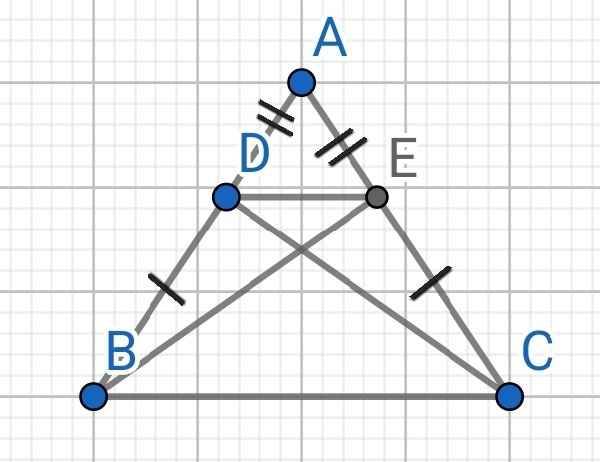a) Xét ∆AEB và ∆ADC có:
AB = AC (gt)
∠A chung
AE = AD (gt)
⇒ ∆AEB = ∆ADC (c-g-c)
⇒ BE = DC (hai cạnh tương ứng)
b) Đề sai, ghi lại đề đi em!
Đúng 0
Bình luận (0)
Cho tam giác ABC . Có AB = AC . Lấy điểm D trên cạnh AB . Lấy điểm E trên cạnh AC sao cho AD = AE a) Chứng minh BE = CD b) Gọi O là giao điểm của BE và CD . Chứng minh rằng tam giác BOD bằng tam giác COE
cho tam giác abc có ab = ac lấy điểm d trên cạnh ab , điểm e trên cạnh ac sao cho ad = ae
a, chứng minh rằng be =cd
b, gọi o là giao điểm của be và cd chứng minh rằng tam giác bod = tam giác coe .
a: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{DAC}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
Suy ra: BE=CF
b: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ODB}=\widehat{OEC}\)
Xét ΔODB và ΔOEC có
\(\widehat{ODB}=\widehat{OEC}\)
BD=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔODB=ΔOEC
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB<AC), vẽ tia phân giác AD của tam giác ABC. Trên cạnh AC lấy điểm E sao cho AE=AB.
a) Chứng minh tam giác ADB = tam giác ADE
b) Chứng minh AD là đường trung trực của BE
c) Gọi F là giao điểm của AB và DE. Chứng minh tam giác BFD=tam giác ECD
d) So sánh DB và DC
Cho tam giác ABC ( AB<AC). Vẽ phân giác AD của tam giác ABC. Trên cạnh AC lấy điểm E sao cho AE=AB
a) Chứng minh tam giác ADB= tam giác ADE
b) Chứng minh AD là đường trung trực của BE
c) Gọi F là giao điểm của AB và DE. Chứng minh tam giác BFD= tam giác ECD
d) So sánh DB và DC
Cho tam giác ABC (AB<AC), vẽ tia phân giác AD của tam giác ABC. Trên cạnh AC lấy điểm E sao cho AE=AB.
a) Chứng minh tam giác ADB=tam giác ADE
b) Chứng minh AD là đường trung trực của BE
c) Gọi F là giao điểm của AB và DE. Chứng minh tam giác BFD=tam giác ECD
d) So sánh DB và DC
a)xet tam giac abd va tam giac aed co
ab=ae
ad la canh chunggoc bad = goc ead
=>tam giác abd = ead
b)gọi i là giao điểm của ad và be
xét tam giác abi và tam giác aei có :
ab=ae
ad là cạnh chung
goc bai = góc eai
=> tam giác abi= tâm giác aei
=>ib=ie =>ad là đường trung trực của be
cho mk 3 đi mk giải tiếp cho, bài nay mk vừa mới kiểm tra
Đúng 1
Bình luận (0)
mk giải tiếp nè
theo câu a,b=>góc dbf= góc dec (kề bù do góc abd= aed)
xét tam giác bfd và ecd có
góc dbf= góc dec
bd=ed
bdf=edc
=> tam giác dbf= tam giác ecd
k cho mk đi.mk hứa mk tl hết cho mà
Đúng 1
Bình luận (0)