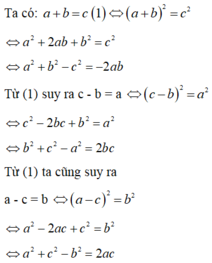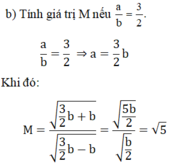Cho 2 số a,b ko đồng thời bằng 0 thì giá trị của M=a2/(1+a2) + b2/(1+b2) + 1/(a2+b2)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
1 Cho biểu thức M a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.2 Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Đọc tiếp
1 Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
2 Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
Đúng 0
Bình luận (0)
Rút gọn: M= (a2+b2+2)3-(a2+b2-2)3-12(a2+b2)2
Cho a + b =1. Hãy tính giá trị của biểu thức N= a3+b3+3ab
\(N=a^3+b^3+3ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\)
=1
Đúng 1
Bình luận (0)
\(M=\left(a^2+b^2+2-a^2-b^2+2\right)\left[\left(a^2+b^2+2\right)^2+\left(a^2+b^2+2\right)\left(a^2+b^2-2\right)+\left(a^2+b^2-2\right)^2\right]-12\left(a^2+b^2\right)^2\\ M=4\left(a^4+b^4+4+4a^2+4b^2+2a^2b^2+\left(a^2+b^2\right)^2-4+a^4+b^4+4-4a^2-4b^2+2a^2b^2\right)-12\left(a^4+2a^2b^2+b^4\right)\\ M=4\left(3a^4+3b^4+4+6a^2b^2\right)-12\left(a^4+2a^2b^2+b^4\right)\\ M=4\left(3a^4+3b^4+4+6a^2b^2-3a^4-6a^2b^2-3b^4\right)\\ M=4\cdot4=164\)
Đúng 3
Bình luận (0)
Cho abc ≠ 0; a + b c. Tính giá trị của biểu thức
B
(a
2
+
b
2
−
c
2
)(b
2
+
c
2
−
a
2...
Đọc tiếp
Cho abc ≠ 0; a + b = c. Tính giá trị của biểu thức B = (a 2 + b 2 − c 2 )(b 2 + c 2 − a 2 )(c 2 + a 2 − b 2 ) 8a 2 b 2 c 2
A. -1
B. 1
C. 2
D. -2
Cho các số thực a,b,c thỏa mãn đồng thời a2+2=b4 , b2+2=c4, c2+2=a4
tĩnh giá trị biểu thức B=a2+b2+c2+a2b2c2-(a2b2+b2c2+c2a2)+2022
Cho a > 0, b > 0 thỏa mãn a + b = 1
Tìm giá trị nhỏ nhất của biểu thức P = (a2 + 1/b2) (b2 + 1/a2)
Cho biểu thức:
M
a
a
2
-
b
2
+
1
+
a
a
2
-
b
2
:
b
a
-...
Đọc tiếp
Cho biểu thức:
M = a a 2 - b 2 + 1 + a a 2 - b 2 : b a - a 2 - b 2 với a > b > 0
b) Tính giá trị M nếu a b = 3 2
cho a,b,c khác 0 ; a+b+c=0 tính a=1/(a2+b2-c2)+1/(b2+c2-a2)+1/(a2+c2-b2)
Câu hỏi của Hattory Heiji - Toán lớp 8 - Học toán với OnlineMath
tvbobnokb' n
iai
ni;bv nn0
Cho ba số a,b,c thỏa mãn đồng thời 3 điều kiện: a2 + 2b + 10; b2 + 2c + 10; c2 + 2a +1 0. Tính giá trị biểu thức: A a2003 + b2009 + c2011.
Đọc tiếp
Cho ba số a,b,c thỏa mãn đồng thời 3 điều kiện: a2 + 2b + 1=0; b2 + 2c + 1=0; c2 + 2a +1 =0. Tính giá trị biểu thức: A= a2003 + b2009 + c2011.
Cho A=1/(b2+c2-a2)+1/(c2+a2-b2)+1/(a2+b2-c2) rút gọn A biết a+b+c=0
Do a+b+c= 0
<=> a+b= -c
=> (a+b)2= c2
Tương tự: (c+a)2= b2, (c+b)2= a2
Ta có: \(A=\frac{1}{b^2+c^2-a^2}+\frac{1}{c^2+a^2-b^2}+\frac{1}{a^2+b^2-c^2}\)
\(=\frac{1}{b^2+c^2-\left(b+c\right)^2}+\frac{1}{c^2+a^2-\left(c+a\right)^2}+\frac{1}{a^2+b^2-\left(a+b\right)^2}\)
\(=\frac{1}{-2bc}+\frac{1}{-2ca}+\frac{1}{-2ab}\)
\(=\frac{a+b+c}{-2abc}=0\)
Đúng 0
Bình luận (0)
A) Rút gọn biểu thức M =(d2+ b2 + 2)3- (a2 + b2 – 2)3 - 12(a2 + b2)2
B)Cho a+b=1. Hãy tính giá trị của biểu thức N = a3 +b3 + 3ab
Mng giải hộ mik với ạ, e cảm ơn, e đang cần gấp á
b: Ta có: \(N=a^3+b^3+3ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\)
\(=1-3ab+3ab\)
=1
Đúng 0
Bình luận (0)