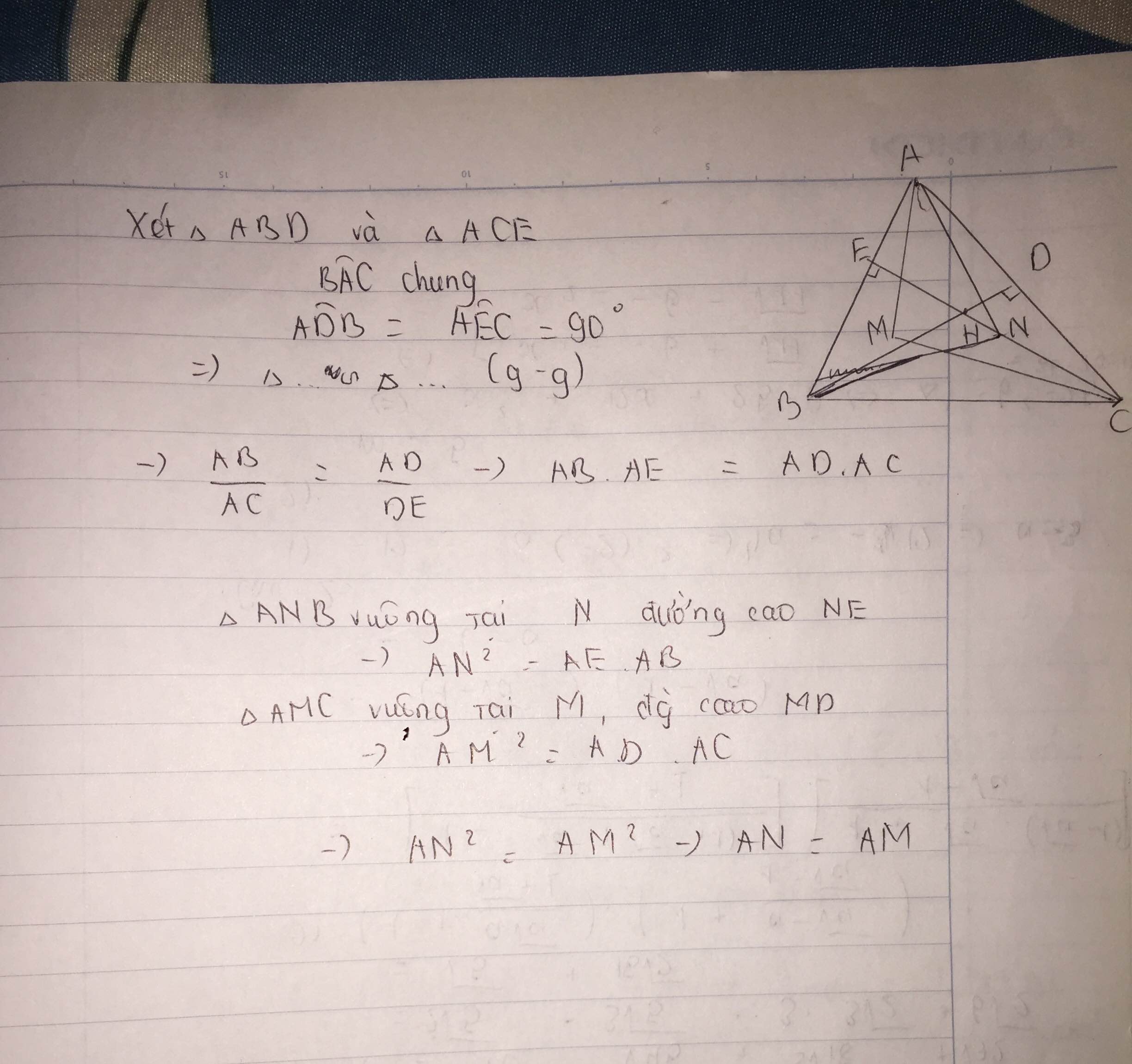Cho tam giác ABC nhọn trực tâm H, trên đoạn BH lấy điểm M và trên đoạn CH lấy điểm N sao cho ^AMC = ^AMC = 90o . Chứng minh rằng AM=AN

Những câu hỏi liên quan
Cho tam giác ABC nhọn, trực tâm H. Trên đoạn BH lấy điểm M và trên đoạn CH lấy điểm N sao cho góc AMC=góc ANB=90. Chứng minh rằng AM = AN
cho tam giác nhọn ABC trực tâm H. Trên các đoạn thẳng HB, HC lần lượt lấy các điểm M,N sao cho \(\widehat{AMB}=\widehat{AMC}=90\). Chứng minh AM= AN.
Cho tam giác ABC nhọn: H là trực tâm. Trên các đoạn HB và HC lấy các điểm M,N sao cho góc AMC= góc ANB=90 độ. Cminh: AM=AN
cho tam giác ABC có 3 góc nhọn . các đường cao BD ,CE cắt nhau tại H
1/ CMR : tam giác ADB ∞ tam giác AEC
2/ CMR : HB.HD=HC.HE
3/ trên các đoạn thẳng BD và CE lấy lần lượt 2 điểm M , N sao cho ∠AMC =∠ANB = 90o .CMR: AM=AN
1: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
2: Xet ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
3: ΔAMC vuông tại M có MD vuông góc AC
nên AD*AC=AM^2
ΔANB vuông tại N có NE vuông góc AB
nên AE*AB=AN^2
=>AM=AN
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn có 2 đường cao BD và CE. Trên đoạn BD lấy M sao cho góc AMC=90. Trên đoạn CE lấy N sao cho AN=AM. Chứng minh góc ANB=90
cho tam giác nhọn ABC, 2 đường cao BD và CE cắt nhau tại H, trên BH và CH lần lượt lấy điểm M và N sao cho góc AMC=góc ANB=90độ. CMR AM=AN
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AD\cdot AC=AB\cdot AE\left(1\right)\)
Xét ΔANB vuông tại N có NE là đường cao ứng với cạnh huyền AB
nên \(AB\cdot AE=AN^2\left(2\right)\)
Xét ΔAMC vuông tại M có MD là đường cao ứng với cạnh huyền AC
nên \(AD\cdot AC=AM^2\left(3\right)\)
Từ (1), (2) và (3) suy ra AM=AN
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn, đường cao BD và CE. Trên đoạn BD lấy M sao cho góc AMC bằng 90 độ. Trên đoạn CE lấy N sao cho góc ANB = 90 độ. Chứng minh AM=AN.
Cho tam giác nhọn ABC, 2 đường cao BD và CE cắt nhau tại H. Trên HB và HC lần lượt lấy các điểm M và N sao cho \(\widehat{AMC}\) = \(\widehat{ANB}\) = \(90^o\). Chứng minh rằng: AM = AN
Theo đề có: `ΔAMC` là Δ vuông, đường cao `MD`.
=> `AM^2=AD.AC` (1)
`ΔANB` là Δ vuông, đường cao `NE`:
=> `AN^2=AE.AB` (2)
Lại có: `ΔABD=ΔACE`(g.g)
=> \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\Leftrightarrow AB.AE=AC.AD\left(3\right)\)
Từ (1), (2), (3) suy ra: `AM=AD` (đpcm)
$HaNa$
Đúng 4
Bình luận (1)
Cho tam giác nhọn ABC. Đường cao BD và CE cắt tại nhau tại H. Trên BD lấy điểm M sao cho góc MAC = 90o ; Trên CE lấy điểm N sao cho góc ANB = 90o . Chứng minh: AM = AN.