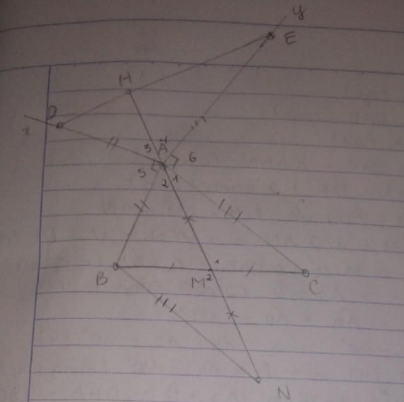
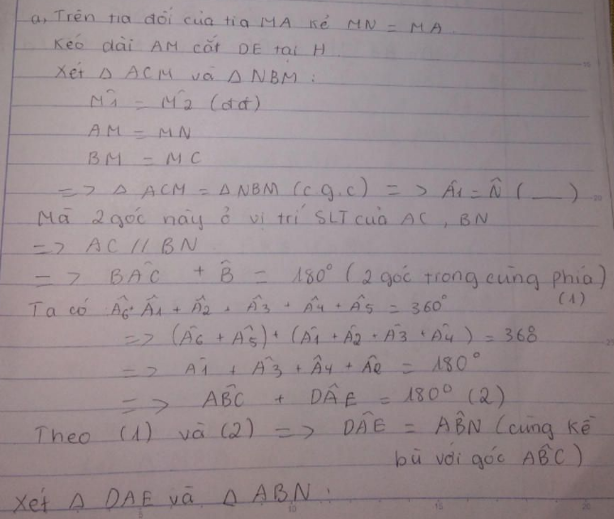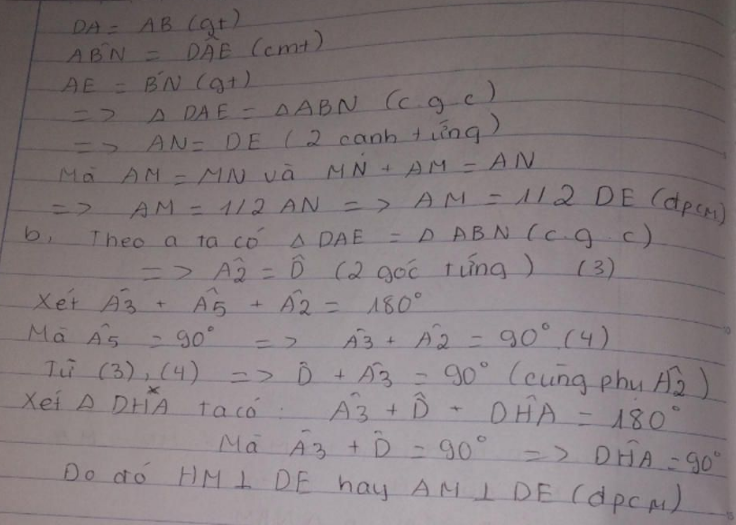Cho tam giác ABC ( AB < AC ) có góc A nhọn . Trên nửa mp bờ AB không chứa điểm C vẽ tia Ax vuông góc với AB , trên đó lấy điểm D sao cho AD = AB . Trên nửa mp bờ AC không chứa điểm B vẽ tia Ay vuông góc với AC sao cho AE = AC. Chứng minh rằng :
a) BE = CD và \(\widehat{ADC}=\widehat{ABE}\)
b) Gọi giao điểm của BE và CD là K . Tính \(\widehat{DKE}\)
c) Gọi M là trng điểm của cạnh BC . CMR : AM vuông góc với ED
d) CMR : \(\widehat{MAB}>\widehat{MAC}\)

Những câu hỏi liên quan
cho tam giác có góc A <90 độ . trên nửa mp bờ AB không chứa điểm C vẽ tia Ax vuông góc với AB, lấy trên Ax điểm D sao cho AD= AB. trên nửa mp bờ chứa tia AC không chứa điểm B ta vẽ tia Ay vuông góc với AC và lấy trên Ay điểm E sao cho AE=AC. chứng minh rằng : a; BE = CD b; BE vuoong góc với CD
c,gọi I là TĐ của BC cmr:DE=2AI
a) Ta có :
AB = AD ( gt ) ( 1 )
CA = AE ( gt ) ( 2 )
Từ ( 1 )( 2 )=>AB+AE = AC + AD
hay BE = CD
Đúng 0
Bình luận (0)
cho tam giác có góc A <90 độ . trên nửa mp bờ AB không chứa điểm C vẽ tia Ax vuông góc với AB, lấy trên Ax điểm D sao cho AD= AB. trên nửa mp bờ chứa tia AC không chứa điểm B ta vẽ tia Ay vuông góc với AC và lấy trên Ay điểm E sao cho AE=AC. chứng minh rằng :
a; BE = CD b; BE vuoong góc với CD
a) ta co:
goc DAB= goc EAC (=90)
goc BAC= goc BAC ( goc chung)
--> goc DAB+goc ABC= goc EAC+ goc BAC
-> goc ADC= goc EAB
xet tam giac DAC va tam giac BAE ta co: AD=AB ( gt ) goc ADC = goc EAB ( cmt ) AC= AE ( gt)--> tam giac DAC = tam giac BAE ( c=g=c)
b_ goi O la giao diem cua DC va AB, I la giao diem BE va DC
taco : goc ADO+ goc AOD=90 ( tam giac DAO vuong tai A )
goc ADO= goc OBI ( tam giac ADC = tam giac ABE )
goc AOD= goc BOI ( 2 goc doi dinh)
--> goc OBI+ goc BOI= 90
xet tam giac BOI taco
goc OBI + goc BOI+ goc BIO= 180 ( tong 3 goc trong tam giac )
ma goc OBI+goc BOI=90 ( cmt)
nen 90 + goc BIO=180
--> goc BIO =180-90=90
--> BI vuong goc OI hay BE vuong goc DC
Đúng 0
Bình luận (0)
a) ta co:
goc DAB= goc EAC (=90)
goc BAC= goc BAC ( goc chung)
--> goc DAB+goc ABC= goc EAC+ goc BAC
-> goc ADC= goc EAB
xet tam giac DAC va tam giac BAE ta co: AD=AB ( gt ) goc ADC = goc EAB ( cmt ) AC= AE ( gt)--> tam giac DAC = tam giac BAE ( c=g=c)
b_ goi O la giao diem cua DC va AB, I la giao diem BE va DC
taco : goc ADO+ goc AOD=90 ( tam giac DAO vuong tai A )
goc ADO= goc OBI ( tam giac ADC = tam giac ABE )
goc AOD= goc BOI ( 2 goc doi dinh)
--> goc OBI+ goc BOI= 90
xet tam giac BOI taco
goc OBI + goc BOI+ goc BIO= 180 ( tong 3 goc trong tam giac )
ma goc OBI+goc BOI=90 ( cmt)
nen 90 + goc BIO=180
--> goc BIO =180-90=90
--> BI vuong goc OI hay BE vuong goc DC
Đúng 0
Bình luận (0)
a) ta co:
goc DAB= goc EAC (=90)
goc BAC= goc BAC ( goc chung)
--> goc DAB+goc ABC= goc EAC+ goc BAC
-> goc ADC= goc EAB
xet tam giac DAC va tam giac BAE ta co: AD=AB ( gt ) goc ADC = goc EAB ( cmt ) AC= AE ( gt)--> tam giac DAC = tam giac BAE ( c=g=c)
b_ goi O la giao diem cua DC va AB, I la giao diem BE va DC
taco : goc ADO+ goc AOD=90 ( tam giac DAO vuong tai A )
goc ADO= goc OBI ( tam giac ADC = tam giac ABE )
goc AOD= goc BOI ( 2 goc doi dinh)
--> goc OBI+ goc BOI= 90
xet tam giac BOI taco
goc OBI + goc BOI+ goc BIO= 180 ( tong 3 goc trong tam giac )
ma goc OBI+goc BOI=90 ( cmt)
nen 90 + goc BIO=180
--> goc BIO =180-90=90
--> BI vuong goc OI hay BE vuong goc DC
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có góc A < 90 . Trên nửa MP bờ AB chứa điểm C vẽ tia Ax vuông góc với AB , trên tia Ax lấy D sao cho AD=AB . Trên nửa MP bờ AC có chứa B vẽ tia Ay vuông góc với AC , trên tia Ay lấy E sao cho Ay lấy E sao cho AE=AC . Gọi M là trung điểm của BC . CMR : AM= DE/2
Vẽ hình luôn nha mấy bạn,tks nak
Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD=AB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE=AC. Chứng minh rằng:
a) AM=DE/2
b)AM vuông góc DE
Cho tam giác ABC. M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD=AB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE=AC. Chứng minh rằng:
a) AM=DE/2
b)AM vuông góc DE
Bài 4. Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy D sao cho ADAB . Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy E sao cho AEAC.Chứng minh rằnga )AMdfrac{1}{2}.DEb)AMperpDE
Đọc tiếp
Bài 4. Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy D sao cho AD=AB . Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy E sao cho AE=AC.
Chứng minh rằng
a )AM=\(\dfrac{1}{2}\).DE
b)AM\(\perp\)DE
Bài 4. Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy D sao cho ADAB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy E sao cho AEACChứng minh rằnga )AM1/2DEb)AM vuông góc với DE
Đọc tiếp
Bài 4. Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy D sao cho AD=AB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy E sao cho AE=AC
Chứng minh rằng
a )AM=1/2DE
b)AM vuông góc với DE
a) Trên tia đối tia MA lấy điểm F sao cho AM = AF (*)
Xét tam giác BFM và tam giác ACM có:
AM = FM (theo *)
Góc BMF = góc AMC (2 góc đối đỉnh)
BM = CM (vì M là trung điểm của BC)
=> Tam giác BFM = tam giác CAM (c.g.c)
=> AC = BF (2 cạnh tương ứng)
Vì AC = AE (gt) nên AE = BF
Ta có: góc F = góc CAM (vì tam giác BFM = tam giác CAM)
Mà 2 góc này ở vị trí so le trong
=> BF // AC (dấu hiệu nhận biết)
=> Góc BAC + góc ABF = 180 độ (2 góc trong cùng phía)
Mà góc BAC + góc DAE = 180 độ
=> Góc DAE = góc ABF
Xét tam giác ABF và tam giác ADE có:
AB = AD (gt)
Góc DAE = góc ABF (chứng minh trên)
AE = BF (2 cạnh tương ứng)
=> Tam giác ADE = tam giác BAF (c.g.c)
=> AF = DE (2 cạnh tương ứng)
Lại có: AM = AF : 2 => AM = DE : 2 (đpcm)
b) Gọi giao điểm của AM và DE là N
Ta có: tam giác ADE = tam giác BAF (chứng minh trên)
=> Góc D = góc BAF (2 góc tương ứng)
Mà góc BAF + góc DAN = 180 độ - góc BAD = 180 độ - 90 độ = 90 độ
=> Góc D + góc DAN = 90 độ
=> Tam giác ADN vuông tại N
hay AM _|_ DE (đpcm)
Đúng 1
Bình luận (0)
Bài 4. Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy D sao cho ADAB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy E sao cho AEACChứng minh rằnga )AM1/2DEb)AM vuông góc với DE nhớ vẽ hình
Đọc tiếp
Bài 4. Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy D sao cho AD=AB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy E sao cho AE=AC
Chứng minh rằng
a )AM=1/2DE
b)AM vuông góc với DE nhớ vẽ hình
Cho ABC có Â 90 độ. Trên nửa mặt phẳng bờ AB không chứa điểm C vẽ tia Ax vuông góc với AB ,trên Ax lấy điểm D sao cho AD AB. Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ tia Ay vuông góc với AC ,trên Ay lấy điểm E sao cho AE AC. a, Chứng minh BE CD. b, Chứng minh BE vuông góc với CD. c,kẻ AH vuông góc với BC ( H thuộc BC), EP vuông góc với AH, DQ vuông góc với AH (P,Q thuộc AH).cm AHEPDQ d, gọi ED cắt AH {K} . cm K là trung điểm của ED
Đọc tiếp
Cho ABC có Â < 90 độ. Trên nửa mặt phẳng bờ AB không chứa điểm C vẽ tia Ax vuông góc với AB ,trên Ax lấy điểm D sao cho AD= AB. Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ tia Ay vuông góc với AC ,trên Ay lấy điểm E sao cho AE = AC. a, Chứng minh BE = CD. b, Chứng minh BE vuông góc với CD. c,kẻ AH vuông góc với BC ( H thuộc BC), EP vuông góc với AH, DQ vuông góc với AH (P,Q thuộc AH).cm AH=EP=DQ d, gọi ED cắt AH = {K} . cm K là trung điểm của ED
Cho tam giác ABC có góc A nhọn. Trên nửa mặt phẳng bờ AB không chứa điểm C. Vẽ tia Ax vuông góc với AC và lấy trên Ax một điểm E sao cho AE =AB. Trên nửa mặt phẳng bờ AC không chứa điểm B ,vẽ tia Ay vuông góc với AC và lấy trên đó điểm F sao cho AF= AC. Chứng minh BF=CE, BF vuông góc với CE.