Cho hình thang ABCD (AB//CD) Gọi O là giao điểm của AC và BD.
b) Qua O kẻ MN // AB (M Î AD, N Î BC). Chứng minh O là trung điểm của MN.
Bài 3. Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của AC và BD.
a) Chứng minh OA . OD = OB . OC
b) Qua O kẻ MN // AB (M thuộc AD; N thuộc BC) . Chứng minh O là trung điểm của MN
a: Xét ΔAOB và ΔCOD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔAOB\(\sim\)ΔCOD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)
b: Xét ΔADC có MO//DC
nên MO/DC=AM/AD(1)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(2)
Xét hình thang ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)
Từ (1), (2) và (3) suy ra OM=ON
hay O là trung điểm của MN
Cho hình thang ABCD ( AB//CD), Gọi M,N lần lượt là trung điểm của AB<CD, O là giao điểm của AC và BD; I là giao điểm của AD,BC
a) chứng minh O,I,M,N thẳng hàng
b) Qua O kẻ đường thẳng song song với AB cắt AD,BC lần lượt tại E,F. Chứng minh OE=OF
alodgdhgjkhukljhkljyutfruftyhf
Cho tam giác ABC cân tại A. Kẻ BD ^ AC, CE ^ AB (D Î AC; E Î AB). Gọi O là giao điểm của BD và CE.
a/ Chứng minh tam giác ADB = D AEC
b/ Chứng minh tam giác BOC cân
c/ Chứng minh ED//BC
d/ Gọi M là trung điểm BC. Chứng minh BC = 2EM.
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
b: Ta có: ΔADB=ΔAEC
nên BD=CE
Xét ΔEBC vuông tạiE và ΔDCB vuông tại D có
BC chung
CE=BD
Do đó:ΔEBC=ΔDCB
Suy ra: \(\widehat{OCB}=\widehat{OBC}\)
hay ΔOBC cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
d: Ta có: ΔEBC vuông tại E
mà EM là đường trung tuyến
nên BC=2EM
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
ˆBADBAD^ chung
Do đó: ΔADB=ΔAEC
b: Ta có: ΔADB=ΔAEC
nên BD=CE
Xét ΔEBC vuông tạiE và ΔDCB vuông tại D có
BC chung
CE=BD
Do đó:ΔEBC=ΔDCB
Suy ra: ˆOCB=ˆOBCOCB^=OBC^
hay ΔOBC cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
d: Ta có: ΔEBC vuông tại E
mà EM là đường trung tuyến
nên BC=2EM
Cho hình thang ABCD (AB // CD, AB < CD) .Gọi O là giao điểm của AC và BD
a) Chứng minh OA/AC = OB/BD ( làm được r)
b) Qua O kẻ đường thẳng // với AD cắt DC ở E, qua O kẻ đường thẳng // với BC cắt DC ở F. Chứng minh DE = CF
c) Gọi I là giao điểm của các đường thẳng AD và OF, J là giao điểm của các đường thẳng BC và OE. Chứng minh IJ//AB
d) Gọi H là giao điểm của AD và BC, K là trung điểm của EF. Chứng minh : H,O,K thẳng hàng
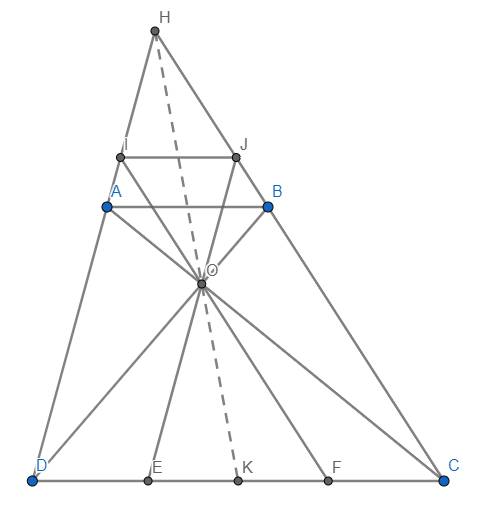
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)
Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)
c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)
Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\)
Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB
d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)
Cho tam giác ABC có AB = AC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. a) Chứng minh: AD = AC. b) Kẻ BH ^ AD ( H Î AD ), kẻ CK ^ AE ( K Î AE). Chứng minh rằng BH = CK và HK//BC c) Gọi O là giao điểm của BH và CK. M là trung điểm BC. Chứng minh rằng ba điểm A, M, O thẳng hàng.
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
b: Xét ΔAHB vuông tại H và ΔACK vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>BH=CK và AH=AK
Xét ΔADE co AH/AD=AK/AE
nên HK//DE
=>HK//BC
c: góc HBD+góc D=90 độ
góc KCE+góc E=90 độ
mà góc D=góc E
nên góc HBD=góc KCE
=>góc OBC=góc OCB
=>OB=OC
=>O nằm trên trung trực của BC(1)
ΔBCA cân tại A
mà AM là trung tuyến
nên AM là trung trực của BC(2)
Từ (1), (2) suy ra A,M,O thẳng hàng
cho hình thang cân ABCD, đáy AB, CD. Biết AC vuông góc BD, khoảng cách từ A-D là 10. Gọi M, N là trung Điểm của AD, BC. Tính MN.( mình kẻ xong hình như bài cho, sau đó lấy O làm giao điểm AC, BD, kẻ thêm đường phụ EF qua O vuông với AB, DC)
Cho hình thang ABCD với AB song song CD, AB<CD. Gọi trung điểm của đường chéo BD là M. Qua M kẻ đường thẳng song song với DC cắt AC tại N. Gọi E là trung điểm của AB, O là giao điểm của AD và BC, OE cắt CD tại F. Chứng minh F là trung điểm của CD.
Cho hình thang cân ABCD AB CD, AD BC , có đáy nhỏ AB. Độ dài đường cao BH bằng độ dài đường trung bình MN M thuộc AD, N thuộc BC của hình thang ABCD. Vẽ BE AC E thuộc DC . Gọi O là giao điểm của AC và BD. Chứng minh rằnga MN DE2 b Tam giác DBE vuông cân