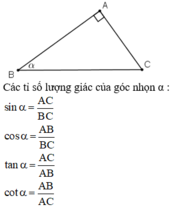
Nêu cách nhớ tỉ số lượng giác của góc nhọn

Những câu hỏi liên quan
Vẽ một tam giác vuông có một góc nhọn 34o rồi viết các tỉ số lượng giác của góc 34o.
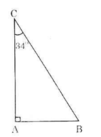
ΔABC vuông tại A có góc C = 34o.
Khi đó:
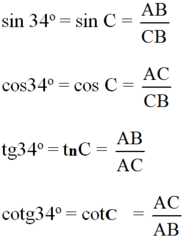
Đúng 0
Bình luận (0)
Vẽ một tam giác vuông có một góc nhọn 34o rồi viết các tỉ số lượng giác của góc 34o.
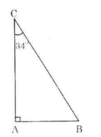
ΔABC vuông tại A có góc C = 34o.
Khi đó:
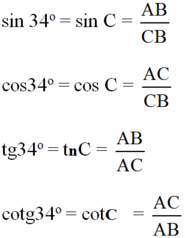
Đúng 0
Bình luận (0)
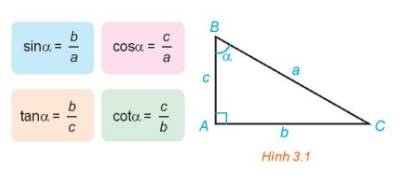
Tam giác ABC vuông tại A có góc nhọn (ABC) ̂ = α. Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn α đã học ở lớp 9.
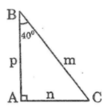
Vẽ một tam giác vuông có một góc nhọn bằng 40 ° rồi viết các tỉ số lượng giác của góc 40 °
cho tam giác ABC vuông tại A, đường cao AH. chứng minh \(AB^2\)= BH.BC (Bằng cách sử dụng tỉ số lượng giác của góc nhọn)
Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao?
Góc \(\alpha \) cho trước,\({0^o} < \alpha < {180^o}\).
Trên nửa đường tròn đơn vị, vẽ điểm \(M({x_o};{y_o})\) sao cho \(\widehat {xOM} = \alpha .\)
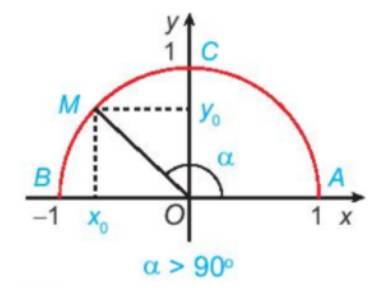
Khi đó:
\(\begin{array}{l}\sin \alpha = {y_o};\\\cos \alpha = {x_o};\\\tan \alpha = \frac{{{x_o}}}{{{y_o}}}\;\;({y_o} \ne 0);\\\cot \alpha = \frac{{{y_o}}}{{{x_o}}}\;\;({x_o} \ne 0).\end{array}\)
Đúng 1
Bình luận (0)
Ta có: \(\widehat{ACM}\) = \(\widehat{ACB}\) -- \(\widehat{MCB}\) = (180o -- 90o -- 45o) -- (180o -- 90o -- 75o) = 30o
Xét △AMC: \(\dfrac{MC}{\sin\widehat{MAC}}\) = \(\dfrac{AM}{\sin\widehat{ACM}}\) (Định lí sin trong tam giác)
⇔ MC = \(\dfrac{AM.\sin\widehat{MAC}}{\sin\widehat{ACM}}\) = \(\dfrac{30.\dfrac{\sqrt{2}}{2}}{\dfrac{1}{2}}\) =
Xét △BMC: \(\sin\widehat{CMB}\) = \(\dfrac{CB}{CM}\) ⇒ CB = CM.\(\sin75\) =
Đúng 0
Bình luận (0)
tìm tỉ số lượng giác của góc nhọn a biết tan a=3
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có: sin 2 α + cos 2 α = 1
Áp dụng định lí pitago trong tam giác vuông OAB có:
OB2 = OA2 + AB2
Từ đó ta có:
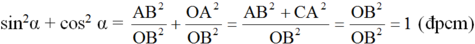
Đúng 0
Bình luận (0)
Sử dụng định nghĩa tỉ số lượng giác của 1 góc nhọn để chứng minh với góc nhọn A tuỳ ý ta có: sin a < 1, cos a <1