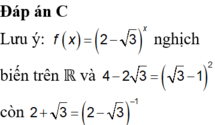a) ĐKXĐ: \(x\notin\left\{\dfrac{1}{3};-\dfrac{1}{3}\right\}\)

Ta có: \(\dfrac{12}{1-9x^2}=\dfrac{1-3x}{1+3x}-\dfrac{1+3x}{1-3x}\)

\(\Leftrightarrow\dfrac{\left(1-3x\right)^2}{\left(1+3x\right)\left(1-3x\right)}-\dfrac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}=\dfrac{12}{\left(1-3x\right)\left(1+3x\right)}\)

Suy ra: \(9x^2-6x+1-9x^2-6x-1=12\)

\(\Leftrightarrow-12x=12\)

hay x=-1(thỏa ĐK)

Vậy: S={-1}

a) Ta có: \(\dfrac{x+5}{3x-6}-\dfrac{1}{2}=\dfrac{2x-3}{2x-4}\)

\(\Leftrightarrow\dfrac{2\left(x+5\right)}{6\left(x-2\right)}-\dfrac{3\left(x-2\right)}{6\left(x-2\right)}=\dfrac{3\left(2x-3\right)}{6\left(x-2\right)}\)

Suy ra: \(2x+5-3x+6=6x-9\)

\(\Leftrightarrow-x+11-6x+9=0\)

\(\Leftrightarrow20-7x=0\)

\(\Leftrightarrow7x=20\)

hay \(x=\dfrac{20}{7}\)(thỏa ĐK)

Vậy: \(S=\left\{\dfrac{20}{7}\right\}\)

a)    \(2\left(9x^2+6x+1\right)=\left(3x+1\right)\left(x-2\right)\)

\(\Leftrightarrow\)\(2\left(3x+1\right)^2-\left(3x+1\right)\left(x-2\right)=0\)

\(\Leftrightarrow\)\(\left(3x+1\right)\left[2\left(3x+1\right)-\left(x-2\right)\right]=0\)

\(\Leftrightarrow\)\(\left(3x+1\right)\left(6x+2-x+2\right)=0\)

\(\Leftrightarrow\)\(\left(3x+1\right)\left(5x+4\right)=0\)

đến đây tự lm nha

b)   \(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\)    (1)

ĐKXĐ:    \(x\ne\pm\frac{1}{3}\)

\(\left(1\right)\)\(\Leftrightarrow\)\(\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2}{\left(1+3x\right)\left(1-3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)

\(\Rightarrow\)\(\left(1-3x\right)^2-\left(1+3x\right)^2=12\)

\(\Leftrightarrow\)\(\left(1-3x-1-3x\right)\left(1-3x+1+3x\right)=12\)

\(\Leftrightarrow\)\(-12x=12\)

\(\Leftrightarrow\)\(x=-1\)   (t/m ĐKXĐ)

Vậy....

a) \(2\left(9x^2+6x+1\right)=\left(3x+1\right)\left(x-2\right)\)

\(\Leftrightarrow2\left(3x+1\right)^2-\left(3x+1\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left(3x+1\right)\left[2\left(3x+1\right)-\left(x-2\right)\right]=0\)

\(\Leftrightarrow\left(3x+1\right)\left(6x+2-x+2\right)=0\)

\(\Leftrightarrow\left(3x+1\right)\left(5x+4\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\5x+4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{3}\\x=-\frac{4}{5}\end{cases}}}\)

b) ĐKXĐ: \(x\ne\pm\frac{1}{3}\)

\(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\)

\(\Leftrightarrow\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)

\(\Leftrightarrow\left(1-3x\right)^2-\left(1+3x\right)^2=12\)

\(\Leftrightarrow\left(1-3x-1-3x\right)\left(1-3x+1+3x\right)=12\)

\(\Leftrightarrow-12x=12\)

\(\Leftrightarrow x=-1\) (thỏa mãn)

Vậy x = -1

a/2(9x²+6x+1)=(3x+1)(x-2)

⇔2(3x+1)²= (3x+1)(x-2)

⇔ 2(3x+1)² :(3x+1)=x-2

⇔ 2(3x+1)=x-2

⇔6x+2-x+2=0

⇔5x+4=0

⇔5x=-4

⇔x=\(\frac{-4}{5}\)

b/\(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\)

⇔\(\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)

⇔12=(1-3x)²-(1+3x)²

⇔-(1-3x-1-3x)(1-3x+1+3x)=--12

⇔-(-6x.2)=-12

⇔12x=-12

⇔x=-1

bạn thấy mình làm sai hay thiếu thì bạn nhớ nhắc mình nha.

giúp mình với ;-;

ghi này chả hiểu j bn ak

ghi rõ ra coi

tui chịu,???

b: \(\Leftrightarrow9x^2+12x+4-18x+12=9x^2\)

=>-6x+16=0

=>-6x=-16

hay x=8/3(nhận)

c: \(\Leftrightarrow\dfrac{x+1+x-1}{\left(x-1\right)\left(x+1\right)}=\dfrac{2}{x+2}\)

\(\Leftrightarrow2x\left(x+2\right)=2\left(x^2-1\right)\)

\(\Leftrightarrow2x^2+4x-2x^2+2=0\)

=>4x+2=0

hay x=-1/2(nhận)

a.

ĐKXĐ: \(x\ge-1\)

\(7+12\sqrt{x+1}=x+4\sqrt{x^2+3x+2}\)

\(\Leftrightarrow4\sqrt{\left(x+1\right)\left(x+2\right)}-12\sqrt{x+1}+x-7=0\)

\(\Leftrightarrow4\sqrt{x+1}\left(\sqrt{x+2}-3\right)+x-7=0\)

\(\Leftrightarrow4\sqrt{x+1}\left(\dfrac{x-7}{\sqrt{x+2}+3}\right)+x-7=0\)

\(\Leftrightarrow\left(x-7\right)\left(\dfrac{4\sqrt{x+1}}{\sqrt{x+2}+3}+1\right)=0\)

\(\Leftrightarrow x-7=0\) (do \(\dfrac{4\sqrt{x+1}}{\sqrt{x+2}+3}+1>0;\forall x\ge-1\))

\(\Rightarrow x=7\)

b.

ĐKXĐ: \(x\ne-\dfrac{1}{3}\)

\(\Rightarrow3x^2+3x+2=\left(3x+1\right)\sqrt{x^2+x+2}\)

\(\Leftrightarrow x^2+x+2-\left(3x+1\right)\sqrt{x^2+x+2}+2x^2+2x=0\)

Đặt \(\sqrt{x^2+x+2}=t\)

\(\Rightarrow t^2-\left(3x+1\right)t+2x^2+2x=0\)

\(\Delta=\left(3x+1\right)^2-4\left(2x^2+2x\right)=\left(x-1\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{3x+1+x-1}{2}=2x\\t=\dfrac{3x+1-\left(x-1\right)}{2}=x+1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+x+2}=2x\left(x\ge0\right)\\\sqrt{x^2+x+2}=x+1\left(x\ge-1\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+x+2=4x^2\left(x\ge0\right)\\x^2+x+2=x^2+2x+1\left(x\ge-1\right)\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{2}{3}\\\end{matrix}\right.\)