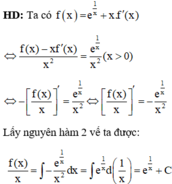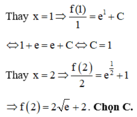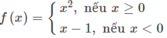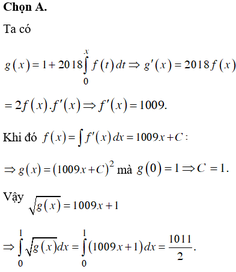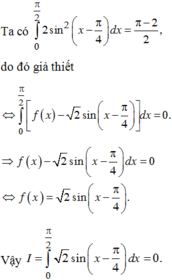Xác định hàm số f(x) thỏa mãn các điều kiện : f(0) = 0; f(2) = 2020 và \(\frac{f\left(x_1\right)}{x_1}=\frac{f\left(x_2\right)}{x_2}\) với \(x_1\)và \(x_2\) là hai giá trị bất kì khác 0 của x.

Những câu hỏi liên quan
Cho hàm số y f(x) xác định và liên tục trên
ℝ
thỏa mãn đồng thời các điều kiện sau:
f
(
x
)
0
,
∀
∈
ℝ
f
x...
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên ℝ thỏa mãn đồng thời các điều kiện sau: f ( x ) > 0 , ∀ ∈ ℝ f ' x = - e x . f 2 x , ∀ ∈ ℝ f 0 = 1 2
Tính giá trị của f(ln2)
A. ln 2 + 1 2
B. 1 4
C. 1 3
D. ln 2 2 + 1 2
Đáp án C
Ta có f ' x = - e x . f 2 x ⇔ f ' x f 2 x = - e x ⇔ ∫ f ' x f 2 x d x = ∫ - e x d x = ∫ d f x f 2 x d x = - e x + C
⇔ - 1 f x = - e x + C ⇔ f x = 1 e x - C mà f 0 = 1 2 ⇒ 1 1 - C = 1 2 ⇒ C = - 1
Vậy f x = 1 e x + 1 ⇒ f ln 2 = 1 e ln 2 + 1 = 1 2 + 1 = 1 3 .
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định với mọi x khác 0,x khác 1 và thỏa mãn điều kiện: f(x) + f(1/(1 - x)) = x
Cho hàm số f(x) xác định và có đạo hàm trên khoảng
0
;
+
∞
, đồng thời thỏa mãn điều kiện
f
1
1
+
e
,
f
x
e
1
x
+
x
.
f
x
,
∀
x...
Đọc tiếp
Cho hàm số f(x) xác định và có đạo hàm trên khoảng 0 ; + ∞ , đồng thời thỏa mãn điều kiện f 1 = 1 + e , f x = e 1 x + x . f ' x , ∀ x ∈ 0 ; + ∞ . Giá trị của f(2) bằng
A. 1 + 2 e
B. 1 + e
C. 2 + 2 e
D. 2 + e
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R
y = f(x) liên tục trên (−∞;0) và trên [0;+∞) nhưng gián đoạn tại x = 0
Gọi f là một hàm xác định trên tập hợp các số nguyên và thỏa mãn ba điều kiện sau
f(0) # 0;
f(1)=3;
f(x)f(y)=f(x+y)+f(x-y)
Tính giá trị của f(7).
theo đề ra ta có f(1)f(0)=f(1+0)+f(1-0) \(\Rightarrow\)3f(0)=3+3\(\Rightarrow\)f(0)=2
f(2)f(0)=f(2+0)+f(2-0) \(\Rightarrow\)2f(2)=2+2\(\Rightarrow\)f(2)=2
f(2)f(1)=f(2+1)+f(2-1) \(\Rightarrow\)2.3=f(3)+3\(\Rightarrow\)f(3)=3
f(3)f(2)=f(3+2)+f(3-2) \(\Rightarrow\)2.3=f(5)+3\(\Rightarrow\)f(5)=3
f(5)f(2)=f(5+2)+f(5-2) \(\Rightarrow\)2.3=f(7)+3\(\Rightarrow\)f(7)=3
Đúng 0
Bình luận (0)
Xét các khẳng định sau i) Nếu hàm số y f(x) xác định trên [-1;1] thì tồn tại
α
∈
-
1
;
1
thỏa mãn
f
(
x
)
≥
f
(
α
)
∀
x
∈
-
1
;
1
. ii) Nếu hàm số y f(x) xác định trên [-1;1] thì tồn...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn f ( x ) ≥ f ( α ) ∀ x ∈ - 1 ; 1 .
ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β ) ∀ x ∈ - 1 ; 1 .
iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn f ( γ ) = 0
Số khẳng định đúng là
A. 3.
B. 2.
C. 1.
D. 0.
Cho hàm số yfleft(xright) liên tục trên tập xác định R, và thỏa mãn điều kiện phương trình fleft(xright)0 có 3 nghiệm x-3 ; x0 ; x2. Xét hàm số ygleft(xright)fleft(x^2+4x-mright), tính tổng các giá trị nguyên của tham số min[-10;10] để phương trình gleft(xright)0 có đúng 5 nghiệm phân biệt .A. -6 B. 42 C. 50 D. 6P/s: Kì thi cuối học kỳ 2 lớp 11 trường THPT Phan Huy Chú , thành phố Hà NộiEm xin nhờ sự...
Đọc tiếp
Cho hàm số \(y=f\left(x\right)\) liên tục trên tập xác định R, và thỏa mãn điều kiện phương trình \(f'\left(x\right)=0\) có 3 nghiệm \(x=-3\) ; \(x=0\) ; \(x=2\). Xét hàm số \(y=g\left(x\right)=f\left(x^2+4x-m\right)\), tính tổng các giá trị nguyên của tham số \(m\in[-10;10]\) để phương trình \(g'\left(x\right)=0\) có đúng 5 nghiệm phân biệt .
A. -6 B. 42 C. 50 D. 6
P/s: Kì thi cuối học kỳ 2 lớp 11 trường THPT Phan Huy Chú , thành phố Hà Nội
Em xin nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán, em cám ơn nhiều ạ!
Cho hàm số yf(x)0 xác định và có đạo hàm trên đoạn [0;1] và thỏa mãn các điều kiện sau: g(x)1+2018
∫
0
x
f
(
t
)
dt
;
g
(
x
)
f
2
(...
Đọc tiếp
Cho hàm số y=f(x)>0 xác định và có đạo hàm trên đoạn [0;1] và thỏa mãn các điều kiện sau: g(x)=1+2018 ∫ 0 x f ( t ) dt ; g ( x ) = f 2 ( x ) . Tính ∫ 0 1 ( g ( x ) dx ?
A. 1011/2.
B. 1009/2.
C. 2019/2.
D. 505
Xác định hàm số f(x) thỏa mãn các điều kiện :
f(0) = 0 và f(2) = 2
\(\frac{f\left(x_1\right)}{x_1}=\frac{f\left(x_2\right)}{x_2}\)với x1, x2 là hai giá trị bất kì khác 0 của x.
Với mọi x khác 0 ta có:
\(\frac{f\left(x\right)}{x}=\frac{f\left(2\right)}{2}=\frac{2}{2}=1\)
=> \(f\left(x\right)=x\)(1)
Với x = 0 thay vào (1) có: f(0) = 0 thỏa mãn
=> f(x) = x thỏa mãn với mọi x
Cho hàm số f(x) xác định, liên tục trên [0;π/2] thỏa mãn điều kiện:
∫
0
π
2
f
2
x
+
2
2
f
x
cos
x
+...
Đọc tiếp
Cho hàm số f(x) xác định, liên tục trên [0;π/2] thỏa mãn điều kiện:
∫ 0 π 2 f 2 x + 2 2 f x cos x + π 4 d x = 2 - π 2
Tích phân ∫ 0 π 2 f x d x bằng
A. π/2
B. 0.
C. 1.
D. π/4