lập bảng giá trị, vẽ đồ thị hàm số y = \(\dfrac{-1}{2}x+2\)

Những câu hỏi liên quan
thiết lập đc bảng giá trị và vẽ đc đồ thị của hàm số
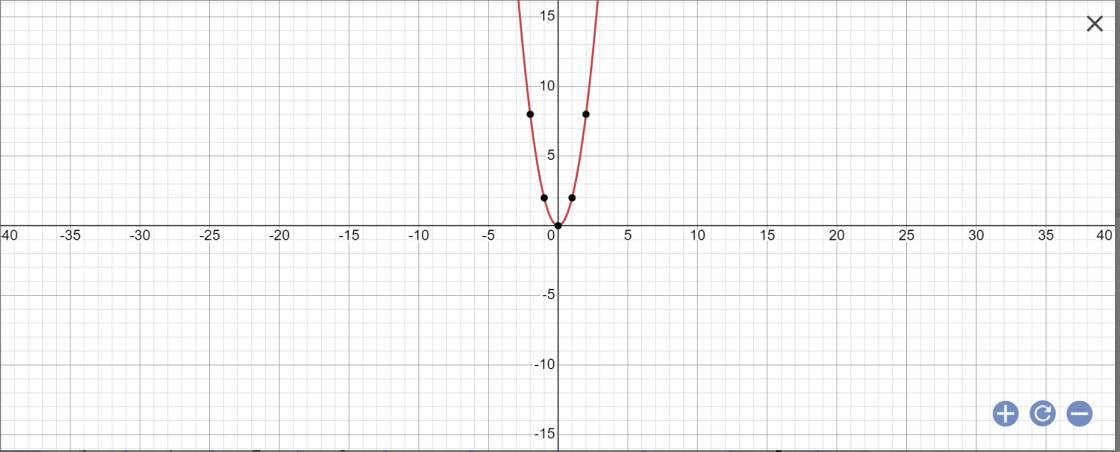
a,y=2x2
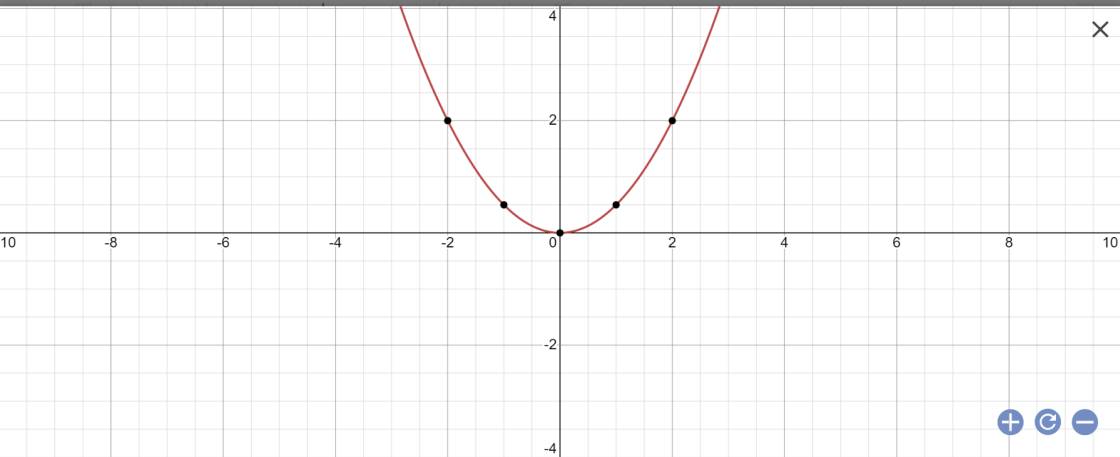
b,y=\(\dfrac{1}{2}x^2\)
1. Cho hàm số y=3x-1. Lập bảng giá trị tương ứng của y khi x= -1, -1/2, 1/2, 1, 3/2
2. a) Vẽ đồ thị hàm số y=1/2x
b) Tính giá trị của x khi y=-1, y=2, y=-0,5
1)Cho hàm số y=3x-1 . Lập bảng giá trị tương ứng của y khi x=-1;-1/2 ; 1/2 ; 1 ; 3/2 2) a) Vẽ đồ thị hàm y = 1/2x b) Tính gía trị của x khi y = -1 ; 2 ; -0.5
1)Cho hàm số y=3x-1 . Lập bảng giá trị tương ứng của y khi x=-1;-1/2 ; 1/2 ; 1 ; 3/2 2) a) Vẽ đồ thị hàm y = 1/2x b) Tính gía trị của x khi y = -1 ; 2 ; -0.5
1)Cho hàm số y=3x-1 . Lập bảng giá trị tương ứng của y khi x=-1;-1/2 ; 1/2 ; 1 ; 3/2 2) a) Vẽ đồ thị hàm y = 1/2x b) Tính gía trị của x khi y = -1 ; 2 ; -0.5
1)Cho hàm số y=3x-1 . Lập bảng giá trị tương ứng của y khi x=-1;-1/2 ; 1/2 ; 1 ; 3/2 2) a) Vẽ đồ thị hàm y = 1/2x b) Tính gía trị của x khi y = -1 ; 2 ; -0.5 ban giup minh voi
3 giờ trước (11:31)
1)Cho hàm số y=3x-1 . Lập bảng giá trị tương ứng của y khi x=-1;-1/2 ; 1/2 ; 1 ; 3/2 2) a) Vẽ đồ thị hàm y = 1/2x b) Tính gía trị của x khi y = -1 ; 2 ; -0.5
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
Đúng 4
Bình luận (0)
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
Đúng 2
Bình luận (0)