Các câu hỏi tương tự
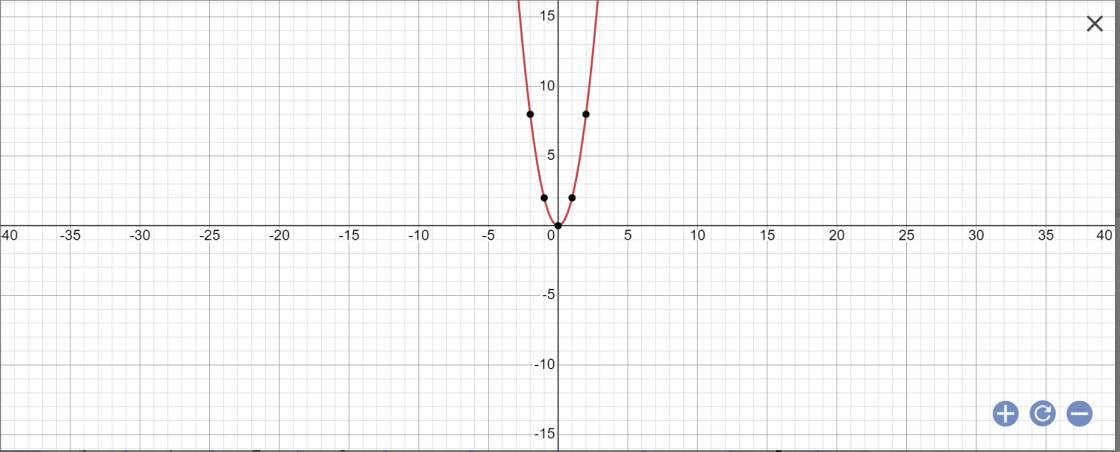
Cho hàm số Y=4x2 (P) và Y=-x+3 (D) a, Vẽ đồ thị hàm số. ( Lập bảng giá trị) b, Xác định tọa độ giao điểm của (P) và (D) bằng phương pháp đại số.
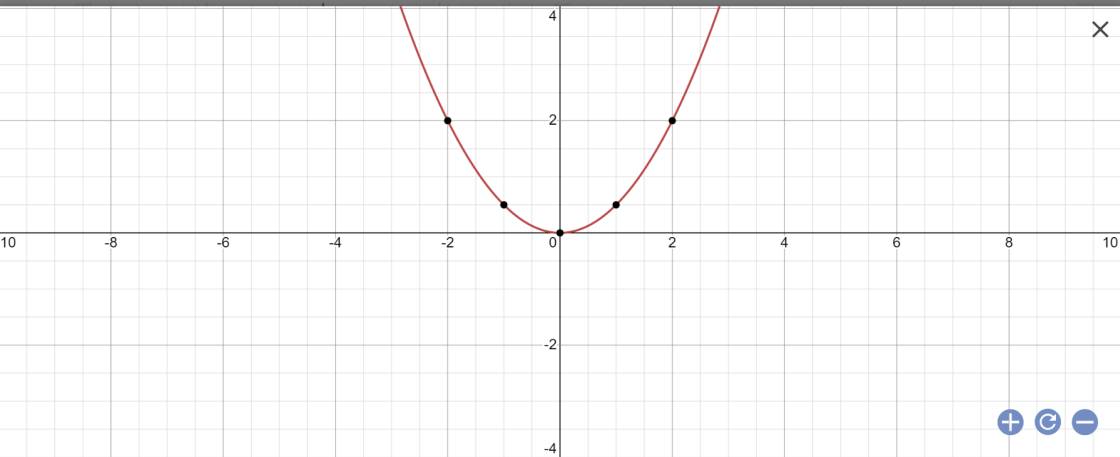
a, Vẽ đồ thị hàm số y=\(\dfrac{1}{2}\)\(^{x^2}\) ( P)
b, Tìm giá trị của m sao cho điểm C (-2;m) thuộc đồ thị (P)
1) biết rằng với x4thif hàm số y 2x+b có giá trị 5a) tìm bb) vẽ đồ thị của hàm số ngs với giá trị của b tìm đc ở câu a2) tìm hệ số a của hàm số y ax+1 biết rằng khi x 1 thì y3+căn x3) xác dịnh hàm số y ã+b biết đồ thị cắt trục tung tại điểm có tung độ 3 và cắt trục hoành độ -24) trên mặt phẳng tọa độ oxy cho 2 điểm A( 1;2) ,B (3,4) a) tìm hệ số a của đg thẳng đi qua avaf bb) xắc định hàm số biết đồ thị của nó là đoạn thằng đi qua a và b
Đọc tiếp
1) biết rằng với x=4thif hàm số y =2x+b có giá trị 5
a) tìm b
b) vẽ đồ thị của hàm số ngs với giá trị của b tìm đc ở câu a
2) tìm hệ số a của hàm số y =ax+1 biết rằng khi x =1 thì y=3+căn x
3) xác dịnh hàm số y= ã+b biết đồ thị cắt trục tung tại điểm có tung độ = 3 và cắt trục hoành độ = -2
4) trên mặt phẳng tọa độ oxy cho 2 điểm A( 1;2) ,B (3,4)
a) tìm hệ số a của đg thẳng đi qua avaf b
b) xắc định hàm số biết đồ thị của nó là đoạn thằng đi qua a và b
Giúp e vs ạ :
a) Vẽ đồ thị hàm số y= \(\dfrac{1}{2}x^2\) (P)
b) Tìm giá trị của m sao cho điểm C(-2;m) thuộc đồ thị (P)
c) Tìm tọa độ giao điểm của đường thẳng y= x - 0,5 và parabol(P)
a) Vẽ đồ thị của hàm số sau y = 2x + 2 b) Cho hai hàm số y = (2k + 2) * x - 3 và y = (1 - 3k) * x + 2 Với giá trị nào của k thi đồ thị của hai hàm số là hai đường thẳng cắt nhau ?
Cho hàm số y=(2m-3)x-1. a) tìm giá trị của m để đồ thị hàm số song song với đường hẳng y=-5x+3. Vẽ đồ thị. b) Tìm giá trị của m để đồ thị hàm số đi qua điểm A(-1;0). c) Tìm giá trị của m để đồ thị của hàm số đã cho và các bạn các đường thẳng y=1 và y=2x-5 đồng qui tại một điểm. Giúp mình giải bài này với.
Câu 1. Với giá trị nào của m thì đồ thị hai hàm số y2x+3 và y (m-1)x+3 là hai đường thẳng trùng nhauA. m-1 B. m2 C. mdfrac{-1}{2} D. m 3Câu 2 Cho hàm số y-mx+2 . Giá trị của m để đồ thị hàm số trên cắt đường thẳng yx+3 tại điểm có hoành độ bằng 1 làA. m -2 B. m 4 C. m -3 D. m 4
Đọc tiếp
Câu 1. Với giá trị nào của m thì đồ thị hai hàm số y=2x+3 và y= (m-1)x+3 là hai đường thẳng trùng nhau
A. m=-1 B. m=2 C. m=\(\dfrac{-1}{2}\) D. m= 3
Câu 2 Cho hàm số \(y=-mx+2\) . Giá trị của m để đồ thị hàm số trên cắt đường thẳng y=x+3 tại điểm có hoành độ bằng 1 là
A. m= -2 B. m = 4 C. m= -3 D. m = 4
a. Tìm tập xác định của hàm số y = \(\frac{x+1}{2x+7}\)
b. Lập bảng biến thiên và vẽ đồ thị hàm số y = x2 + 3x + 2.
Cho hàm số y = f(x) = 1/2x^2 có đò thị là (P)
a) Tính f(-2).
b) Vẽ đồ thị (P) ( câu này em tự làm đc).
c) Cho hàm số y = 2x +6 có đờ thị là (d). Tìm tọa độ giao điểm của hai đồ thị (P) và (d).
Mn giúp em.