Cho tam giác ABC nội tiếp đường tròn (O). Một đường thẳng song song với tiếp tuyến tại C cắt cạnh AC ở D và cạnh BC ở E. Chứng tỏ hai tam giác ABC và tam giác EDC đồng dạng và CA.CD=CB.CE

Những câu hỏi liên quan
,Cho tam giác ABC nội tiếp đường tròn (O). Một đường thẳng song song với tiếp tuyến tại C cắt cạnh AC ở D và cạnh BC ở E. Chứng minh CA.CD=CB.CE
Xét ΔCDE và ΔCBA có
góc CDE=góc CBA
góc C chung
=>ΔCDE đồng dạng với ΔCBA
=>CD/CB=CE/CA
=>CD*CA=CB*CE
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn (O), tia phân giác của góc A cắt đường tròn ở M. Tiếp tuyến kẻ từ M với đường tròn cắt các tia AB và AC lần lượt tại D và E. Chứng minh: a/ BC song song với DE b/ Tam giác AMB đồng dạng tam giác MCE c/ Tam giác AMC đồng dạng tam giác MDB d/ Nếu AC=CE thì MA^2 = MD.ME
Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh:a)
B
D
2
A
D
.
C
D
b) Tứ giác BCDE là tứ giác nội tiếpc) BC song song với DE
Đọc tiếp
Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh:
a) B D 2 = A D . C D
b) Tứ giác BCDE là tứ giác nội tiếp
c) BC song song với DE
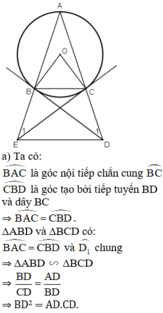
b) ΔABC cân tại A
⇒ AB = AC
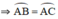
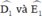 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
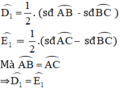
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).
Đúng 0
Bình luận (0)
Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh:a)
B
D
2
A
D
.
C
D
b) Tứ giác BCDE là tứ giác nội tiếpc) BC song song với DE
Đọc tiếp
Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh:
a) B D 2 = A D . C D
b) Tứ giác BCDE là tứ giác nội tiếp
c) BC song song với DE
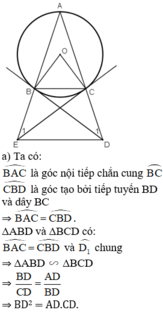
b) ΔABC cân tại A
⇒ AB = AC
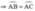
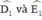 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
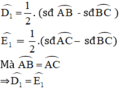
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại B có AB < AC nội tiếp trong đường tròn (O). Gọi (d) là tiếp tuyến với đường tròn tại điểm A. Một đường thẳng song song với (d) cắt các cạnh AB, AC và đường thẳng BC lần lượt tại D, E và I. a) Chứng minh rằng số do hai cung nhỏ BA và BC bằng nhau. b) Chứng minh rằng góc ABC = AED. c) Chứng minh tứ giác BCED nội tiếp. d) Chứng minh rằng IB.IC =
a: góc BAC=góc BCA
=>sđ cung BC=sđ cung BA
b: xy//DE
=>góc AED=góc yAE=góc ABC
c: góc AED=góc ABC
=>góc ABC+góc DEC=180 độ
=>BCDE nội tiếp
Đúng 1
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn (O), tia phân giác của góc A cắt đường tròn ở M. Tiếp tuyến kẻ từ M với đường tròn cắt các tia AB và AC lần lượt tại D và E. Chứng minh:
a/ BC song song với DE
b/ Tam giác AMB đồng dạng tam giác MCE
c/ Tam giác AMC đồng dạng tam giác MDB
d/ Nếu AC=CE thì MA^2 = MD.ME
Cho tam giác ABC nội tiếp đường tròn o phân giác góc A cắt BC tại D cắt đt tại M chứng minh BM bính phương bằng MD.MA
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). D là điểm thuộc cạnh BC (D khác B và D khác C).Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F. Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M. Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N. 2) Giả sử
F
N
E
M
B
N...
Đọc tiếp
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O).
D là điểm thuộc cạnh BC (D khác B và D khác C).
Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F.
Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M.
Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N.
2) Giả sử F N E M = B N C M . Chứng minh rằng AD là phân giác của tam giác ABC.

2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .
Đúng 0
Bình luận (0)
cho tam giac ABC nội tiếp đường tròn tâm O phân giác BAC cắt đường tròn O ở M. Tiếp tuyến kẻ từ M với đường tròn cắt các tia AB và AC lần lượt ở D và E.CM a) BC song song với DE b)tam giác AMB đồng dạng với tam giác MCE, tam giác AMC đồng dạng với tam giác MDB c) Nếu AC=CE thì MA^2=MD.ME
cho tam giác ABC nội tiếp đường tròn (O), xy là tiếp tuyến tại A của đường tròn. Một đường thẳng song song với xy cắt các cạnh AB, AC lần lượt tại D và E. chứng minh tứ giác BDEC là tứ giác nội tiép












