b) ΔABC cân tại A
⇒ AB = AC
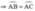
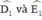 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
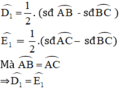
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

b) ΔABC cân tại A
⇒ AB = AC
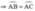
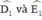 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
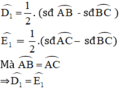
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).
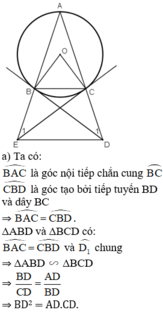
Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh:
a) B D 2 = A D . C D
b) Tứ giác BCDE là tứ giác nội tiếp
c) BC song song với DE
Cho ∆ABC cân tại A, có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn O. Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB tại D và E. Chứng minh rằng:
a) BD2 = AD.CD
b) Tứ giác BCDE là tứ giác nội tiếp
c) BC || DE
Cho tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên nội tiếp đtròn (O). Tiếp tuyến tại B và C của đtròn lần lượt cắt tia AC và tia AB ở D và E. CMR:
a) BD2 = AD.CD
b) Tứ giác BCDE nt
c) BC // DE
cho tam giác ABC cân tại A ,có cạnh đáy nhỏ hơn cạnh bên và nội tiếp đường tròn tâm O .tiếp tuyến tại B; C của đường tròn lần lượt cắt AC và AB ở D và E .chứng minh
a) BD2=AD.AC
B) Tứ giác BCDE nội tiếp
c) BC // DE
Cho tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (o), Tiếp tuyến Bvà C của đường tròn lần lượt cắt ti AC và AB ở D và E . CM:
a,tam giác ADB = tam giác BEC
b, Bốn điểm B,C,D,E cùng thuộc 1 đường tròn
c,BC // DE
Cho tam giác ABC nội tiếp đường tròn (O), tia phân giác của góc A cắt đường tròn ở M. Tiếp tuyến kẻ từ M với đường tròn cắt các tia AB và AC lần lượt tại D và E. Chứng minh: a/ BC song song với DE b/ Tam giác AMB đồng dạng tam giác MCE c/ Tam giác AMC đồng dạng tam giác MDB d/ Nếu AC=CE thì MA^2 = MD.ME
cho tam giác ABC nội tiếp đường tròn (O), xy là tiếp tuyến tại A của đường tròn. Một đường thẳng song song với xy cắt các cạnh AB, AC lần lượt tại D và E. chứng minh tứ giác BDEC là tứ giác nội tiép
bài 1: Cho tam giác MNP cân tại M có đáy nhỏ hơn cạnh bên. Tam giác nội tiếp (O) bán kính R. Tiếp tuyến tại N và P của đường tròn lần lượt cắt tia MP, MN tại E và D. Hỏi:
a, chứng minh NE bình = EP. EM
b, Chứng minh tứ giác DEPN nội tiếp.
bài 2: Cho (O), lấy A không thuộc đường tròn. Đường thẳng AO giao với (O) tại B, C (AB < AC). Qua A vẽ đường thẳng không đi qua O cắt (O) tại 2 điểm D và E (AD < AE). Đường vuông góc với AB tại A cắt đường thẳng CE tại F.
a, Chứng minh tứ giác ABEF nội tiếp
b, Gọi M là giao điểm thứ 2 của FB với (O). Chứng minh DM vuông góc AC.
c, CE . CF + AD . AE = AC bình
Cho tam giác ABC cân tại A nội Tiếp đường tròn tâm O. Gọi D và H lần lượt là trung điểm các cạnh AC, BC. tiếp tuyến của đường tròn tâm O tại điểm A cắt tia BD tại E tia CE cắt đường tròn tâm O tại điewmr thứ hai là F a/ chứng minh đường thang BC song song với đường thẳng AE b/ chứng minh tứ giác ABCE Là hình bình hành c/ chứng minh bốn điểm O, H, C, D, cùng thuôc một đường tròn d/ gọi I trung điểm CF, G giao điểm BC và OI . CMR GH=2AH.HO/BC
Giúp mình với