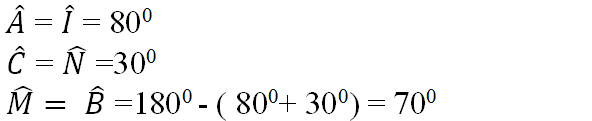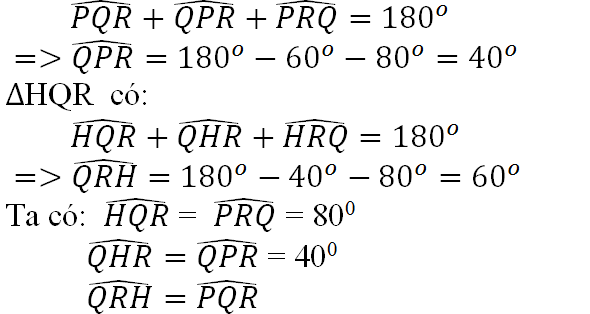bài 45 của luyện tập về ba trường hợp bằng nhau của tam giác trong sgk toán lp 7 tập 1 trang125

Những câu hỏi liên quan
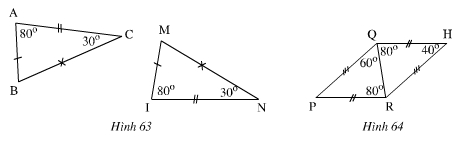
Tìm trong các hình 63, 64 các tam giác bằng nhau ( các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau ). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó .
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ
Đúng 0
Bình luận (0)
hinh 63
dinh A = dinh I
dinh C = dinh N
dinh B = dinh M
\(\Rightarrow\)tam giac \(ABC=\)tam giac \(IMN\)
hinh 64
dinh P = dinh H
dinh chua goc \(\widehat{PQR}=\)dinh chua goc \(\widehat{QRH}\)
dinh chua goc \(\widehat{PRQ}=\)dinh cua goc \(\widehat{RQH}\)
\(\Rightarrow\)tam giac \(PQR=\)tam giac \(HRQ\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
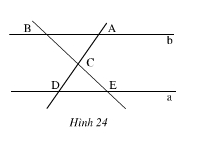
Cho hình 24 (a // b). Hãy nêu tên các cặp góc bằng nhau của hai tam giác CAB và CDE.
Vì a // b nên hai tam giác CAB và CDE có:
Chứng minh định lí 2,3 của bài CÁC TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC VUÔNG ( SGK TRANG 83 - TẬP 2 LỚP 8 )
Ai giúp mình với :)) Ai giải xong mình like cmt cho nhé :*
Tu kehinh nhe
Vitamgiac ABCdong đáng với tam giác A'B'C' gocB=goc B' 1
Ma gocH=gocH' 2
Tu 1va 2 suy ra
Tam giac ABHdongdang voitam giacA'B'H'
suy ra AH/A'H'=AB/A'B'=k
Đúng 0
Bình luận (0)
Định lí 2. Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng = tỉ số đồng dạng
Hình ở SGK
Vì ΔA'B'C' ~ ΔABC => \(\hept{\begin{cases}\frac{A'B'}{AB}=k\\\widehat{B'}=\widehat{B}\end{cases}}\)
Xét ΔA'H'B' và ΔAHB có : \(\hept{\begin{cases}\widehat{H'}=\widehat{H}\left(=90^0\right)\\\widehat{B'}=\widehat{B}\left(cmt\right)\end{cases}}\)=> ΔA'H'B' ~ ΔAHB (g.g)
=> \(\frac{A'H'}{AH}=\frac{H'B'}{HB}=\frac{A'B'}{AB}=k\left(đpcm\right)\)
giải hộ mk bài 43/sgk1/t125 nha( luyện tập về 3 trường hợp bằng nhau của tam giác)
a) ∆OAD và ∆OCB có: OA= OC(gt)
∠O chung
OB = OD (gt)
OAD = OCB (c.g.c) AD = BC
Nên ∆OAD=∆OCB(c.g.c)
suy ra AD=BC.
b)
Ta có ∠A1 = 1800 – ∠A2
∠C1 = 1800 – ∠C2
mµ ∠A2 = ∠C2 do ΔOAD = ΔOCB (c/m trên)
⇒ ∠A1 = ∠C1
Ta có OB = OA + AB
OD = OC + CD mà OB = OD, OA = OC ⇒ AB = CD
Xét ΔEAB = ΔECD có:
∠A1 = ∠C1 (c/m trên)
AB = CD (c/m trên)
∠B1 = ∠D1 (ΔOCB = ΔOAD)
⇒ ΔEAB = ΔECD (g.c.g)
c) Xét ΔOBE và ΔODE có:
OB = OD (GT)
OE chung
AE = CE (ΔAEB = ΔCED) ⇒ΔOBE = ΔODE (c.c.c)
⇒ ∠AOE = ∠COE ⇒ OE là phân giác của góc ∠xOy.
Đúng 0
Bình luận (0)
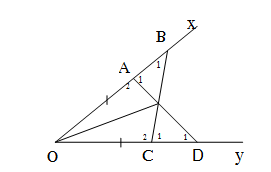
Bài 43. Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA<OB.
Lấy các điểm C,D thuộc tia Oy sao cho OC=OA, OD=OB. Gọi E là giao điểm của AD và BC.
Chứng minh rằng:
a) AD=BC;
b) ∆EAB=∆ECD;
c )OE là tia phân giác của xOy.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Có ai đăng đề bài tập trong SGK toán lp 7 giùm mik với
Bài 3 phép nhân vs phép chia số hữu tỉ nha![]()
Đúng 0
Bình luận (0)
Bài 3 (trang 106 SGK Toán 5) Luyện tập chung : Một sợi dây nối hai bánh xe ròng rọc. Đường kính của bánh xe là 0,35m. Hai trục cách nhau 3,1m. Tính độ dài sợi dây.
Độ dài hai phần uốn cong của sợi dây chính là hai nửa chu vi của bánh xe nên đúng bằng chu vi của bánh xe.
Độ dài hai phần thẳng của sợi dây đều bằng khoảng cách giữa hai trục.
Độ dài hai phần uốn cong của sợi dây là:
0,35 x 3,14 = 1,099 (m)
Độ dài hai phần thẳng của sợi dây là:
3,1 x 2 = 6,2 (m).
Độ dài sợi dây là:
1,099 + 3,1 x 2 = 7,299 (m)
Đáp số: 7,299m
Đúng 0
Bình luận (0)
Độ dài hai phần uốn cong của sợi dây là:
0,35 x 3,14 = 1,099 (m)
Độ dài hai phần thẳng của sợi dây là:
3,1 x 2 = 6,2 (m)
Độ dài sợi dây là: 1,099 + 3,1 x 2 = 7,299 (m)
Đáp số: 7,299m
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải bài Mặt phẳng toạ độ ( SGK Toán 7 )
Bài tập + Luyện tập
( 3 tick cho bài )
Mặt phẳng toạ độ - Toán 7 - Loigiaihay.com
Đúng 0
Bình luận (0)
https://h7.net/toan-7/bai-6-mat-phang-toa-do-l572.html
Đúng 0
Bình luận (0)
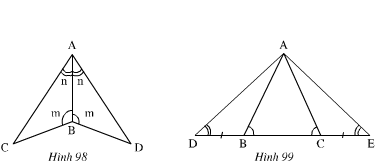
Bài 34 (trang 123 SGK Toán 7 Tập 1): Trên mỗi hình 98, 99 có các tam giác nào bằng nhau? Vì sao?
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
Đúng 0
Bình luận (0)
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
Đúng 0
Bình luận (0)
Bài 34. Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?
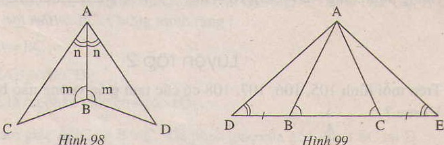
Giải:
Xem hình 98)
∆ABC và ∆ABD có:
^A1=^A2(gt)
AB là cạnh chung.
^B1=^B2(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
^B1+^B2=1800 (Hai góc kề bù).
^C1+ ^C2=1800 (Hai góc kề bù)
Mà ^B2=^C2(gt)
Nên ^B1=^C1
* ∆ABD và ∆ACE có:
^B1=^C1(cmt)
BD=EC(gt)
ˆD = ˆE(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆD=ˆE(gt)
^C2=^B2(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Hãy cho một số bài toán ( Ktra1 tiết ) về tam giác cân , các trường hợp bằng nhau của tam giác và lời giải của bài đó