Cho một điểm m bất kì trong hình chữ nhật ABCD. Chứng minh:
MA2+MC2=MB2+MC2
Những câu hỏi liên quan
Bài 1. Cho hình chữ nhật ABCD, M là một điểm bất kì thỏa mãn AMB ̂ =900
. Chứng minh rằng MA2 + MB2 + MC2 + MD2 không đổi
Bài 2. Cho đường tròn (O,R), P là điểm cố định nằm trong đường tròn.
Qua P kẻ 2 dây cung AB và CD vuông góc với nhau.
1) Chứng minh PA2 + PB2 + PC2 + PD2 không đổi
2) Gọi M là trung điểm của AC. Chứng minh PM vuông góc với BD
Cho hình vuông ABCD cạnh a . Tìm tập hợp M sao cho :
2 MA2 + MB2 = MC2 + MD2
Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho:
M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị cực tiểu.
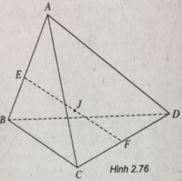
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:
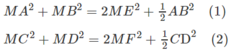
Cộng (1) và (2) ta có:
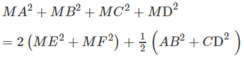
Gọi J là trung điểm của EF, ta có:
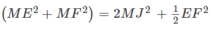
Khi đó:
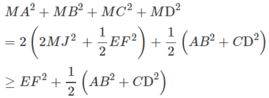
Vậy M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị nhỏ nhất khi M ≡ J.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại B và M thuộc miền trong tam giác sao cho góc BMC =135 độ. Chứng minh MA2=2.MB2+MC2
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng A.
7
a...
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng T = M A 2 + M B 2 + M C 2 + M D 2 nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng
A. 7 a 15 15
B. a 15 2
C. a 15 3
D. 4 a 15 15
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng T = M A 2 + M B 2 + M C 2 + M D 2 nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng
Cho A(1; 2), B(-3; 1) và C(4; -2). Tìm tập hợp các điểm M sao cho MA2 + MB2= MC2
Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm
A
1
;
0
;
0
,
B
0
;
2
;
0
,
C
0
;
0
;
3
. Tập hợp các điểm M thỏa...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A 1 ; 0 ; 0 , B 0 ; 2 ; 0 , C 0 ; 0 ; 3 . Tập hợp các điểm M thỏa M A 2 = M B 2 + M C 2 là mặt cầu có bán kính
A. R = 2
B. R = 3
C. R = 3
D. R = 2
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm
A
1
;
0
;
0
,
B
0
;
2
;
0
,
C
0
;
0
;
3
.
Tập hợp các điểm M thỏa...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A 1 ; 0 ; 0 , B 0 ; 2 ; 0 , C 0 ; 0 ; 3 . Tập hợp các điểm M thỏa M A 2 = M B 2 + M C 2 là mặt cầu có bán kính
A. R = 2
B. R = 3
C. R = 3
D. R = 2
Đáp án D
Ta có: M B 2 + M C 2 − M A 2 = M B → 2 + M C → 2 − M A → 2 = M I → + I B → 2 + M I → + I C → 2 − M I → + I A → 2
= M I 2 + 2 M I → I B → + I C → − I A → + I B 2 + I C 2 − I A 2
Gọi I là điểm thỏa mãn I B → + I C → − I A → = 0 → ⇒ I − 1 ; 2 ; 3
Suy ra M B 2 + M C 2 − M A 2 = M I 2 + I B 2 + I C 2 − I A 2 = 0 ⇔ M I = I A 2 − I B 2 − I C 2 = 2
Đúng 0
Bình luận (0)
Cho tứ diện ABCD đều có cạnh bằng a và trọng tâm G. Tập hợp các điểm M thỏa mãn
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
11
a
2
2
là mặt cầu
Đọc tiếp
Cho tứ diện ABCD đều có cạnh bằng a và trọng tâm G. Tập hợp các điểm M thỏa mãn M A 2 + M B 2 + M C 2 + M D 2 = 11 a 2 2 là mặt cầu
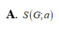
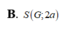
