Ta có: \(P=\dfrac{\sqrt{a}+3}{\sqrt{a}-2}-\dfrac{\sqrt{a}-1}{\sqrt{a}+2}+\dfrac{4\sqrt{a}}{4-\sqrt{a}}\)

a) ĐKXĐ: \(a\ne4;a\ne16;a\ge0\)

\(P=\dfrac{\sqrt{a}+3}{\sqrt{a}-2}-\dfrac{\sqrt{a}-1}{\sqrt{a}+2}-\dfrac{4\sqrt{a}}{\sqrt{a}-4}\)

\(P=\dfrac{\left(\sqrt{a}+3\right)\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}-\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}-\dfrac{4\sqrt{a}}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)

\(P=\dfrac{a+3\sqrt{a}+2\sqrt{a}+6-a+2\sqrt{a}+\sqrt{a}-2-4\sqrt{a}}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\)

\(P=\dfrac{4\sqrt{a}+4}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\)

\(P=\dfrac{4\sqrt{a}+4}{a-4}\)

b) Thay x=9 vào P ta có:

\(P=\dfrac{4\cdot\sqrt{9}+4}{9-4}=\dfrac{16}{5}\)

c) \(P< 0\) khi:

\(\dfrac{4\sqrt{x}+4}{a-4}< 0\) 

Mà: \(4\sqrt{x}+4>0\)

\(\Rightarrow a-4< 0\)

\(\Rightarrow a< 4\) 

kết hợp với Đk ta có:

\(0\le x< 4\)

a: \(A=\dfrac{x+15+2x-6}{\left(x+3\right)\left(x-3\right)}=\dfrac{3x+9}{\left(x+3\right)\left(x-3\right)}=\dfrac{3}{x-3}\)

a) Ta có: \(A=\left(1+\dfrac{x^2}{x^2+1}\right):\left(\dfrac{1}{x-1}-\dfrac{2x}{x^3+x-x^2-1}\right)\)

\(=\dfrac{2x^2+1}{x^2+1}:\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)

\(=\dfrac{2x^2+1}{x^2+1}\cdot\dfrac{\left(x-1\right)\left(x^2+1\right)}{\left(x-1\right)^2}\)

\(=\dfrac{2x^2+1}{x-1}\)

b) Thay \(x=-\dfrac{1}{2}\) vào A, ta được:

\(A=\left(2\cdot\dfrac{1}{4}+1\right):\left(\dfrac{-1}{2}-1\right)\)

\(=\dfrac{3}{2}:\dfrac{-3}{2}=-1\)

c) Để A<1 thì A-1<0

\(\Leftrightarrow\dfrac{2x^2+1}{x-1}-1< 0\)

\(\Leftrightarrow\dfrac{2x^2+1-x+1}{x-1}< 0\)

\(\Leftrightarrow\dfrac{2x^2-x+2}{x-1}< 0\)

\(\Leftrightarrow x-1< 0\)

hay x<1

a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)

\(=\left(2x\right)^3-1^3-7x^3-7\)

\(=8x^3-1-7x^3-7=x^3-8\)

b: Thay x=-1/2 vào A, ta được:

\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)

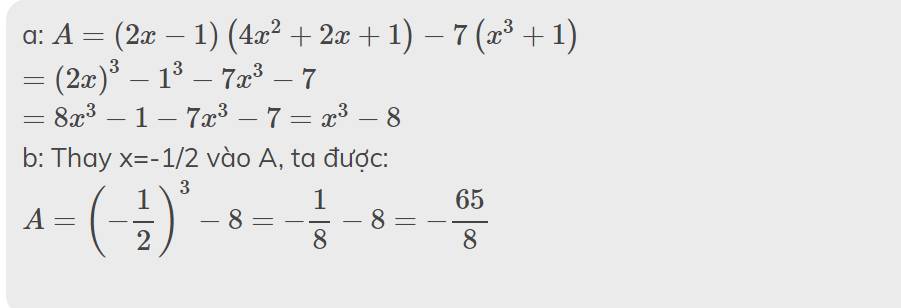
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)

Để A là số nguyên tố thì x-2=1

=>x=3

a.

TH1: 2x+1>=0 => x >=1/2

=>5x-2-(2x+1)

=5x-2-2x-1

=3x-2

TH2:2x+1<0 => x <1/2

=>5x-2- [-(2x-1)]

=5x-2+2x-1

=7x-3

Vậy A=3x-2 khi x>=1/2

      A=7x-3 khi x<1/2

b.TH1:x>=1/2

=>A=3x-2

Ta có :

2=3x-2

3x=4

x=4/3 (chọn vì x >= 1/2)

TH2:x <1/2

=>A= 7x-3

Ta có:

2=7x-3

7x=5

=>x=5/7 (loại vì x <1/2)

Vậy x=4/3 thì A=2

ĐKXĐ: \(x\ne\pm1;x\ne0\)

a)\(\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right):\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\left(\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\right):\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\dfrac{x^2+2x+1-\left(x^2-2x+1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\dfrac{4x}{\left(x-1\right)\left(x+1\right)}:\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\dfrac{4x}{\left(x-1\right)\left(x+1\right)}.\dfrac{5\left(x-1\right)}{2x}-\dfrac{x^2-1}{x^2+2x+1}\)

\(=\dfrac{10}{x+1}-\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x+1\right)^2}\)

\(=\dfrac{10}{x+1}-\dfrac{x-1}{x+1}\)

\(=\dfrac{11-x}{x+1}\)

b) \(A=\dfrac{11-x}{x+1}=2\)

\(\Leftrightarrow11-x=2\left(x+1\right)\)

\(\Leftrightarrow11-x=2x+2\)

\(\Leftrightarrow-x-2x=2-11\)

\(\Leftrightarrow-3x=-9\)

\(\Leftrightarrow x=3\left(nhận\right)\)

c) -Để \(A=\dfrac{11-x}{x+1}\in Z\) thì:

\(\left(11-x\right)⋮\left(x+1\right)\)

\(\Rightarrow\left(12-x-1\right)⋮\left(x+1\right)\)

\(\Rightarrow12⋮\left(x+1\right)\)

\(\Rightarrow\left(x+1\right)\inƯ\left(12\right)\)

\(\Rightarrow\left(x+1\right)\in\left\{1;2;3;4;6;12;-1;-2;-3;-4;-6;-12\right\}\)

\(\Rightarrow x\in\left\{2;3;5;11;-2;-3;-4;-5;-7;-13\right\}\)

a) đk: x khác 0;2;-2;3

A = \(\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)

= \(\left(\dfrac{2+x}{2-x}+\dfrac{4x^2}{\left(2-x\right)\left(2+x\right)}-\dfrac{2-x}{2+x}\right):\dfrac{x-3}{2x-x^2}\)

= \(\left(\dfrac{\left(x+2\right)^2+4x^2-\left(2-x\right)^2}{\left(2-x\right)\left(2+x\right)}\right):\dfrac{x-3}{x\left(2-x\right)}\)

= \(\dfrac{x^2+4x+4+4x^2-x^2+4x-4}{\left(2-x\right)\left(2+x\right)}.\dfrac{x\left(2-x\right)}{x-3}\)

= \(\dfrac{4x^2+8x}{\left(2-x\right)\left(2+x\right)}.\dfrac{x\left(2-x\right)}{x-3}\)

= \(\dfrac{4x\left(x+2\right)}{\left(2-x\right)\left(2+x\right)}.\dfrac{x\left(2-x\right)}{x-3}=\dfrac{4x^2}{x-3}\)

b) Có \(\left|x-5\right|=2\)

<=> \(\left[{}\begin{matrix}x-5=2< =>x=7\left(Tm\right)\\x-5=-2< =>x=3\left(L\right)\end{matrix}\right.\)

Thay x = 7 vào A, ta có:

\(A=\dfrac{4.7^2}{7-3}=49\)

c) A = \(\dfrac{4x^2}{x-3}⋮4\left(\forall x\right)\)