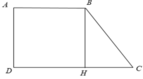
Cho hình thang vuông ABCD ( AB//CD ) có
∠A=∠D= 90o , AB = 2cm, CD = 4cm, ∠C = 45o.
Tính SABCD
Tính diện tích hình thang vuông ABCD ( góc A = góc D = 90o ), biết góc C = 45o, AB = 2cm, CD = 4cm.
Cho hình thang \(ABCD\) có \(\widehat{A}\)=\(\widehat{D}\)=90o, \(\widehat{C}\)= 45o. Biết đường cao của hình thang bằng 4cm, \(AB+CD=10cm\). Tính 2 đáy.
Kẻ đường cao BE ứng với CD \(\Rightarrow BE=4\left(cm\right)\)
Trong tam giác vuông BCE ta có:
\(\widehat{EBC}=90^0-\widehat{C}=90^0-45^0=45^0\)
\(\Rightarrow\widehat{EBC}=\widehat{C}\Rightarrow\Delta BCE\) vuông cân tại E
\(\Rightarrow EC=BE=4\left(cm\right)\)
Tứ giác ABED là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AB=DE\)
Ta có:
\(AB+CD=10\left(cm\right)\)
\(\Leftrightarrow AB+DE+EC=10\)
\(\Leftrightarrow2AB+4=10\)
\(\Rightarrow AB=3\left(cm\right)\)
\(\Rightarrow DE=AB=3cm\Rightarrow CD=DE+EC=7\left(cm\right)\)
Cho hình thang vuông ABCD có A ^ = D ^ = 90 o , AB = AD = 2 cm , CD = 2 AB . Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB
A. 40 π 3 cm 3
B. 16 π 3 cm 3
C. 8 πcm 3
D. 8 π 3 cm 3
Đáp án A
Ta có thể tích khối tròn xoay tạo thành bằng hiệu thể tích hình trụ bán kính đáy AD, chiều cao CD trừ cho thể tích nón đỉnh B, bán kính đáy BM chiều cao CM.
Ta có
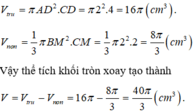
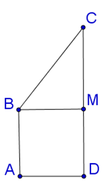
Cho hình thang vuông ABCD có A ^ = D ^ = 90 o , AB=AD=2cm, CD=2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
![]()
![]()
![]()
![]()
Chọn B
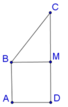
Ta có thể tích khối tròn xoay tạo thành bằng hiệu
thể tích hình trụ bán kính đáy AD, chiều cao
CD trừ cho thể tích nón đỉnh B, bán kính đáy
BM chiều cao CM.
Ta có:

Cho hình thang vuông ABCD A ^ = D ^ = 90 0 , trong đó có C ^ = 45 0 , AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
A. 3 c m 2
B. 8 c m 2
C. 4 c m 2
D. 6 c m 2
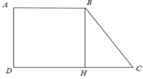
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.

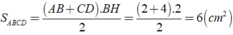
Chọn đáp án D.
Cho hình thang vuông ABCD A ^ = D ^ = 90 0 , trong đó có C ^ = 45 0 , AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
A. 3 c m 2
B. 8 c m 2
C. 4 c m 2
D. 6 c m 2
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.

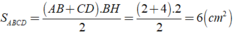
Chọn đáp án D.
Bài 8: cho hình thang vuông ABCD có góc A = góc D = 90o . AB = AD = 2cm, DC = 4cm. Tính hai góc còn lại của hình thang
Bài 8: Cho hình thang ABCD vuông (AB//CD, A = 900) Có AB = 2cm; CD = 4cm, C =300 , kẻ BH vuông góc với CD tại H.
Tính HD; CH; BH; BC?
cho hình thang ABCD (AB//CD) có: AB=4cm;BD=6cm;CD=9cm.Gọi I là giao điểm của AC và BD hỏi:
Tính SABCD biết SABD= 16cm vuông
Cho hình thang vuông ABCD (A = D = 90 ∘ ) có AB = 1cm, CD = 4cm, BD = 2cm. Chọn kết luận sai?
A. ΔABD ~ ΔBDC
B. BDC = 90 ∘
C. BC = 2AD
D. BD vuông góc BC
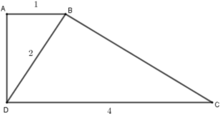
ΔABD và ΔBDC có: ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD)
Và A B B D = B D D C (vì 1 2 = 2 4 )
Do đó ΔABD ~ ΔBDC (c.g.c) nên A đúng.
=> ABD = BDC < 90 ∘ nên B sai.
ΔABD ~ ΔBDC => A B B D = A D B C = 1 2 (cạnh t/u) BC = 2AD nên C đúng.
BAD = DBC = 90 ∘ nên BD ⊥ BC hay D đúng
Vậy chỉ có B sai.
Đáp án: B