ai trả lời đi chứ

a) 3A=2B ; 4B=3C

=> A/2=B/3; B/3=C/4

  Mẫu số chung của B là 9

=> A/2.3=B/3.3; B/3.3=C/4.3

=> A/6=B/9=C/12

=> Ta có: A/6=B/9=C12 = A+B+C =180 độ

                                   = 6+9+12 = 27

=> 180/27=20/3

   => A/6=20/3=6.20/3=40

   => B/9=20/3.9=60

   => C/12=20/3.12=80

Vậy A=40 

      B=60

      C=80

\(2\widehat{A}=3\widehat{B}=6\widehat{C}\Rightarrow\frac{2\widehat{A}}{6}=\frac{3\widehat{B}}{6}=\frac{6\widehat{C}}{6}\Rightarrow\frac{\widehat{A}}{3}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{1}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+2+1}=\frac{180^o}{6}=30^o\)

=> \(\hept{\begin{cases}\frac{\widehat{A}}{3}=30^o\\\frac{\widehat{B}}{2}=30^o\\\frac{\widehat{C}}{1}=30^o\end{cases}}\Rightarrow\hept{\begin{cases}\widehat{A}=90^o\\\widehat{B}=60^o\\\widehat{C}=30^o\end{cases}}\)

Góc A=32.(72)

Góc B=49.(09)

Góc C=98.(18)

a) x⁴+x³+2x²+x+1=(x⁴+x³+x²)+(x²+x+1)=x²(x²+x+1)+(x²+x+1)=(x²+x+1)(x²+1)

b)a³+b³+c³-3abc=a³+3ab(a+b)+b³+c³ -(3ab(a+b)+3abc)=(a+b)³+c³-3ab(a+b+c)

=(a+b+c)((a+b)²-(a+b)c+c²)-3ab(a+b+c)=(a+b+c)(a²+2ab+b²-ac-ab+c²-3ab)=(a+b+c)(a²+b²+c²-ab-ac-bc)

c)Đặt x-y=a;y-z=b;z-x=c

a+b+c=x-y-z+z-x=o

đưa về như bài b

d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung

e)x²(y-z)+y²(z-x)+z²(x-y)=x²(y-z)-y²((y-z)+(x-y))+z²(x-y)

=x²(y-z)-y²(y-z)-y²(x-y)+z²(x-y)=(y-z)(x²-y²)-(x-y)(y²-z²)=(y-z)(x²-2y²+xy+xz+yz)

A nhó

A. góc A bằng 40*; góc B bằng 60*; góc C bằng 80*

Câu A

Theo đề bài, ta có:

(Nếu như vậy thì thường là \(\widehat{C}=90\)thì    \(\widehat{A}+\widehat{B}=\widehat{C}=90\)

Áp dụng tính chất của dãy tỉ số bằng nhau;

\(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{2}=\frac{\widehat{A}+\widehat{B}}{3+2}=\frac{90}{5}=18\)

Do đó:

\(\widehat{A}=54\)

Vậy   \(\widehat{A}=54\)

Ta có: A + B = C

Mặt khác ta lại có: 2A=3B

hay A x\(\frac{2}{3}\)= B

Trong tam giác ABC ta có: A+B+C= 180⁰

hay: A + A x\(\frac{2}{3}\)+A +A x\(\frac{2}{3}\)= 180⁰

A x (1+\(\frac{2}{3}\)+1 +\(\frac{2}{3}\)) =180⁰

^{A x \(\frac{10}{3}\)=}180⁰

^A= 180^{0 : \(\frac{10}{3}\)}

^A= 54⁰

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).

Theo định lí tổng ba góc của tam giác ta có:

    a + b + c = 180.

Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:

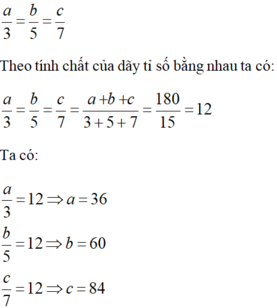
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o