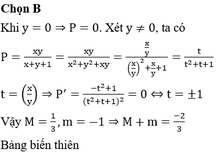cho biểu thức M=x2-5x+y2+xy-4y+2016.với giá trị nào của x,y thì M đạt giá trị nhỏ nhất

Những câu hỏi liên quan
Cho biểu thức : M = x2 – 5x + y2 + xy – 4y + 2019.
Với giá trị nào của x, y thì M đạt giá trị nhỏ nhất ? Tìm giá trị nhỏ nhất đó.
2.M = 2x2 – 10x + 2y2 + 2xy – 8y + 4038 = (x2 – 10x + 25) +( y2 + 2xy + y2) + ( y2 – 8y + 16) + 3997
= (x-5)2 + (x+y)2 + (y - 4)2 + 3997 = N + 3997
Áp dụng bất đẳng thức Bu- nhi a: (ax+ by + cz)2 \(\le\) (a2+ b2 + c2). (x2 + y2 + z2). Dấu bằng xảy ra khi a/x = b/y = c/z
Ta có: [(5 - x).1 + (x+ y).1 + (y + 4).1]2 \(\le\) [(5 - x)2 + (x+y)2 + (y - 4)2 ].(1+ 1+1) = N .3 = 3.N
<=> 92 = 81 \(\le\) 3.N => N \(\ge\) 27 => 2.M \(\ge\) 27 + 3997 = 4024
=> M \(\ge\)2012
vậy Min M = 2012
khi 5 - x = x+ y = y + 4 => x = 4 ; y = -3
Đúng 0
Bình luận (0)
Cho biểu thức M=x^2-5x+y^2+xy-4y+2012 với giá trị nào của x,y thì M đạt GTNN. Tìm GT đó
M=(x+y/2-5/2)^2+2.5y/4-4y-25/4-y^2/4+(y^2-4y+2012) (kiem tra phan nay len lam nhap rut gon luon)
M=(x+y/2-5/2)^2+3/4(y^2-10y+25)+(2012-25/4-3.25/4)
M=(x+y/2-5/2)^2+3/4.(y-5)^2+(.....)
GTNN=(.....)
tai: y=5
2x+5-5=0=> x=0
Đúng 0
Bình luận (0)
Câu 1. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 2. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 3. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Hãy giải ba câu hỏi này
Bài 2:
Ta có: M = a2+ab+b2 -3a-3b-3a-3b +2001
=> 2M = ( a2 + 2ab + b2) -4.(a+b) +4 + (a2 -2a+1)+(b2 -2b+1) + 3996
2M= ( a+b-2)2 + (a-1)2 +(b-1)2 + 3996
=> MinM = 1998 tại a=b=1
Câu 3:
Ta có: P= x2 +xy+y2 -3.(x+y) + 3
=> 2P = ( x2 + 2xy +y2) -4.(x+y) + 4 + (x2 -2x+1) +(y2 -2y+1)
2P = ( x+y-2)2 +(x-1)2+(y-1)2
=> MinP = 0 tại x=y=1
Bài1:
Ta có: a2+ b2+c2+d2= a.(b+c+d)
=> a2+b2+c2+d2 -ab -ac -ad =0
=> 4a2+ 4b2+4c2+4d2-4ab -4ac -4ad=0
=> ( a2 - 4ab +4b2) + ( a2- 4ac + 4c2) +( a2 -4ad+ 4d2) + a2=0
=> ( a-2b)2 + ( a-2c)2 + (a-2d)2 + a2 =0
=> ....
KL: a=b=c=d=0
Biết \(xy=1\) và \(|x+y|\) đạt giá trị nhỏ nhất. Tính giá trị của biểu thức sau:
\(M=\frac{3}{4}+\left(\sqrt{5x^{2016}+4y}+2\right)^{2017}-\frac{x^{2015}}{y^{2016}}\)
Có \(\left(x-y\right)^2\ge0\)
\(\Rightarrow\left(x+y\right)^2\ge4xy\)
\(\Rightarrow\left(x+y\right)^2\ge4\) (Vì xy = 1)
\(\Rightarrow|x+y|\ge2\)
Dấu "=" xả ra khi \(\orbr{\begin{cases}x=y=1\\x=y=-1\end{cases}}\)
Xét x = y = 1 ta được:
\(M=\frac{3}{4}+\left(\sqrt{5.1^{2016}+4.1}-2\right)^{2017}-\frac{1^{2015}}{1^{2016}}\)
\(M=\frac{3}{4}\)
Xét x = y = -1 ta được:
\(M=\frac{3}{4}+\left(\sqrt{5.\left(-1\right)^{2016}+4.\left(-1\right)}\right)^{2017}-\frac{\left(-1\right)^{2015}}{\left(-1\right)^{2016}}\)
\(M=\frac{7}{4}+3^{2017}\)
Vậy với \(xy=1\)và \(|x+y|\)đạt giá trị nhỏ nhất thì M nhận 2 giá trị là \(\orbr{\begin{cases}M=\frac{3}{4}\\M=\frac{7}{4}+3^{2017}\end{cases}}\)
Đúng 0
Bình luận (0)
Có |x+y| lớn hơn hoặc bằng
|x|+|y| dấu bằng sảy ra <=>
xy lớn hơn hoặc bằng 0
mà xy=1 => |x+y|=|x|+|y| (1)
Ta lại có:|x|+|y|-2\(\sqrt{xy}=\)\(\left(\sqrt{x}-\sqrt{y}\right)^2\)Lớn hơn hoặc bằng 0
=>|x|+|y| lớn hơn hoặc bằng \(2\sqrt{xy}=2\left(2\right)\)
Từ (1) và (2)
=>|x+y| lớn hơn hoặc bằng 2
=>MIN |x+y|=2
Dấu bằng sảy ra
<=>|x+y|=2
Hay |x|+|y|=\(2\sqrt{xy}\)
=>\(\left(\sqrt{x}-\sqrt{y}\right)^2=0\)
=>\(\sqrt{x}=\sqrt{y}\Rightarrow x=y\)
Mà |x+y|=2
TH1: x+y=2=>x=y=1
Thay vào M ta tính được M=3/4
TH2:x+y=-2 => x=y=-1
Thay vào M ta được
M=3/4
Vậy: M=3/4
Đúng 0
Bình luận (0)
với giá trị nào của x thì biểu thức M=x2+2x-(2+x)(4-2x+x2)+x3 đạt giá trị nhỏ nhất
\(M=x^2+2x-8-x^3+x^3=x^2+2x-8=\left(x^2+2x+1\right)-9=\left(x+1\right)^2-9\ge-9\)
\(minM=-9\Leftrightarrow x=-1\)
Đúng 1
Bình luận (0)
\(M=x^2+2x-8-x^3+x^3=\left(x^2+2x+1\right)-9=\left(x+1\right)^2-9\ge-9\\ M_{min}=-9\Leftrightarrow x=-1\)
Đúng 1
Bình luận (0)
Với giá trị nào của x, y thì biểu thức: A = /x - y/ + /x + 1/ + 2016 đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Với giá trị nào của x,y thì biểu thức : A=|x-y|+|x+1|+2016 đạt giá trị nhỏ nhất.Tìm giá trị nhỏ nhất đó
Vì |x-y| \(\ge\)0 với mọi x,y;|x+1|\(\ge\)0 vs mọi x
=>A\(\ge\)2016 vs mọi x,y
=> A đạt giá trị nhỏ nhất khi:\(\hept{\begin{cases}\left|x-y\right|=0\\\left|x+1\right|=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=0\\x+1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=y\\x=-1\end{cases}}\)
vậy với x=y=-1 thì A đạt giá trị nhỏ nhất là 2016
k mik nha
bài này mik từng làm rồi
-----Chúc hok tốt---------
Đúng 0
Bình luận (0)
Cho
x
;
y
∈
R
thỏa mãn
x
+
y
≠
-
1
và
x
2
+
y
2
+
x
y
x
+
y
+
1
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P
x
y...
Đọc tiếp
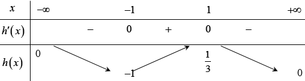
Cho x ; y ∈ R thỏa mãn x + y ≠ - 1 và x 2 + y 2 + x y = x + y + 1 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x y x + y + 1 . Tính M + m
A . 1 3
B . - 2 3
C . 1 2
D . - 1 3
Cho số phức
z
x
+
y
i
(
x
,
y
∈
R
)
thỏa mãn
z
-
2
+
i
z
+
2
+
5
i
và biểu thức
H
x...
Đọc tiếp
Cho số phức z = x + y i ( x , y ∈ R ) thỏa mãn z - 2 + i = z + 2 + 5 i và biểu thức H = x 2 + y 2 - 3 y + 1 x 2 + y 2 + 2 x - 2 y + 2 x 2 + y 2 - 2 x - 4 y + 5 đạt giá trị nhỏ nhất. Giá trị của 2x + y bằng
A. -6
B. - 6 + 5
C. - 3 - 5
D. - 6 - 5