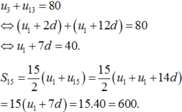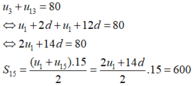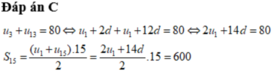cho (Un) là cấp số cộng U3 +U13=80 .tổng 15 số hạng đầu tiên của cấp số cộng đố bằng bao nhiêu

Những câu hỏi liên quan
Cho
u
n
là cấp số cộng biết
u
3
+
u
13
80
Tổng 15 số hạng đầu tiên của cấp số cộng bằng? A. 800. B. 570. C. 600. D. 630.
Đọc tiếp
Cho u n là cấp số cộng biết u 3 + u 13 = 80 Tổng 15 số hạng đầu tiên của cấp số cộng bằng?
A. 800.
B. 570.
C. 600.
D. 630.
Cho u n là cấp số cộng có u 3 + u 13 = 80 . Tổng 15 số hạng đầu tiên của cấp số cộng đó bằng:
A. 800
B. 630
C. 570
D. 600
Đáp án D
Phương pháp:
Sử dụng công thức số hạng tổng quát của cấp số cộng u n = u 1 + n − 1 d và công thức tổng n số hạng đầu tiên của cấp số cộng S n = u 1 + u n . n 2
Cách giải:
Gọi cấp số công có công sai d.

Đúng 0
Bình luận (0)
Cho
u
n
là cấp số cộng biết
u
3
+
u
13
80.
Tổng 15 số hạng đầu của cấp số cộng đó bằng: A. 800 B. 570 C. 600 D. 630
Đọc tiếp
Cho u n là cấp số cộng biết u 3 + u 13 = 80. Tổng 15 số hạng đầu của cấp số cộng đó bằng:
A. 800
B. 570
C. 600
D. 630
Cho
u
n
là cấp số cộng biết
u
3
+
u
13
80
. Tổng 15 số hạng đầu của cấp số cộng đó bằng A. 800 B. 570 C. 600 D. 630
Đọc tiếp
Cho u n là cấp số cộng biết u 3 + u 13 = 80 . Tổng 15 số hạng đầu của cấp số cộng đó bằng
A. 800
B. 570
C. 600
D. 630
Cho cấp số cộng (Un) có
u
5
-
15
,
u
20
60
. Tổng của 10 số hạng đầu tiên của cấp số cộng này là A.
S
10
-
125
B.
S
10
-
250
C.
S
10...
Đọc tiếp
Cho cấp số cộng (Un) có u 5 = - 15 , u 20 = 60 . Tổng của 10 số hạng đầu tiên của cấp số cộng này là
A. S 10 = - 125
B. S 10 = - 250
C. S 10 = 200
D. S 10 = - 200
Cho cấp số cộng
(
u
n
)
có
u
5
-
15
,
u
20
60
. Tổng của 10 số hạng đầu tiên của cấp số cộng này là: A....
Đọc tiếp
Cho cấp số cộng ( u n ) có u 5 = - 15 , u 20 = 60 . Tổng của 10 số hạng đầu tiên của cấp số cộng này là:
A. S 10 = - 125
B. S 10 = - 250
C. S 10 = 200
D. S 10 = - 200
Chọn đáp án A
Gọi u 1 , d lần lượt là số hạng đầu và công sai của cấp số cộng
Ta có: u 5 = - 15 u 20 = 60 .
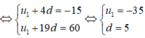
Vậy S 10 = 10 2 . ( 2 u 1 + 9 d ) = - 125
Đúng 0
Bình luận (0)
Cho cấp số cộng
u
n
có
u
5
-
15
,
u
20
60
.
Tổng
S
20
của 20 số hạng đầu tiên của cấp số cộng là A.
S
20
600 B.
S
20
60 C.
S...
Đọc tiếp
Cho cấp số cộng u n có u 5 = - 15 , u 20 = 60 . Tổng S 20 của 20 số hạng đầu tiên của cấp số cộng là
A. S 20 = 600
B. S 20 = 60
C. S 20 = 250
D. S 20 = 500
Cho cấp số cộng
(
u
n
)
có
u
5
-
15
,
u
20
60
. Tổng
S
20
của...
Đọc tiếp
Cho cấp số cộng ( u n ) có u 5 = - 15 , u 20 = 60 . Tổng S 20 của 20 số hạng đầu tiên của cấp số cộng là
A. S 20 = 600
B. S 20 = 60
C. S 20 = 250
D. S 20 = 500
Cho cấp số cộng (un)thoả u2=3 và u10=-15 Tính số hạng đầu u1, công sai d và tổng 20 số hạng đầu tiên của cấp số cộng (un)
\(\left\{{}\begin{matrix}u_1+d=3\\u_1+9d=-15\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=\dfrac{21}{4}\\d=-\dfrac{9}{4}\end{matrix}\right.\)
\(S_{20}=\dfrac{21}{4}.20+\dfrac{19.20}{2}.\left(-\dfrac{9}{4}\right)=-\dfrac{645}{2}\)
Đúng 1
Bình luận (0)