Chọn đáp án A
Gọi u 1 , d lần lượt là số hạng đầu và công sai của cấp số cộng
Ta có: u 5 = - 15 u 20 = 60 .
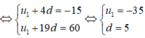
Vậy S 10 = 10 2 . ( 2 u 1 + 9 d ) = - 125
Chọn đáp án A
Gọi u 1 , d lần lượt là số hạng đầu và công sai của cấp số cộng
Ta có: u 5 = - 15 u 20 = 60 .
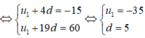
Vậy S 10 = 10 2 . ( 2 u 1 + 9 d ) = - 125
Cho cấp số cộng (un) có u 5 = - 15 , u 20 = 60 . Tổng của 10 số hạng đầu tiên của (un) bằng
A. S10 = -125
B. S10 = -250
C. S10 = 200
D. S10 = -200
Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n , n ∈ ℕ * . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 67 .
B. u 10 = 61 .
C. u 10 = 59 .
D. u 10 = 55 .
Cho cấp số cộng ( u n ) với số hạng đầu u 1 = - 6 và công sai d = 4. Tính tổng S của 14 số hạng đầu tiên của cấp số cộng đó
A.S = 46
B. S = 308
C. S = 644
D. S = 280
Cho cấp số cộng ( u n ) có u 5 = - 15 , u 20 = 60 . Tổng S 20 của 20 số hạng đầu tiên của cấp số cộng là
A. S 20 = 600
B. S 20 = 60
C. S 20 = 250
D. S 20 = 500
1) cho cấp số cộng \(\left(u_n\right)\) có \(\left\{{}\begin{matrix}u_2=4\\u_4=10\end{matrix}\right.\) tính tổng của 10 số hạng đầu tiên cấp số cộng
2) cho cấp số cộng \(\left(u_n\right)\) có \(\left\{{}\begin{matrix}u_3=6\\u_5=16\end{matrix}\right.\) tính tổng của 12 số hạng đầu tiên cấp số cộng
Cấp số cộng (un) có u1 = -1, u10 = 21. Tổng 10 số hạng đầu của cấp số cộng đó bằng
A. 200
B. 110
C. 220
D. 100
Cho cấp số cộng ( u n ) có công thức tổng quát là u n = 5 - 2 n , n ∈ ℕ * . Tính tổng 20 số hạng đầu tiên của cấp số cộng.
A. -350
B. 440
C. -320
D. -340
Tổng n số hạng đầu tiên của một cấp số cộng là S_n = \frac{3n^2 + 13n}{2}Sn=23n2+13n với n \in \mathbb{N}^*n∈N∗. Số hạng tổng quát của cấp số cộng là