P=\(\frac{5}{x-4}\)
tìm giá trị lớn nhất của M =P( 6x2 - 11x + 12 - x3 )
Những câu hỏi liên quan
Cho hàm số
f
(
x
)
x
3
-
6
x
2
+...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 6 x 2 + 11 x - 6 x 2 - 9 k h i x ≠ ± 3 m - 2 3 k h i x = 3 . Tìm giá trị của m để hàm số liên tục tại x=3?
A.8/3
B.2/3
C.1
D.4/3
Cho hàm số
f
(
x
)
x
3
-
6
x
2
+...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 6 x 2 + 11 x - 6 k h i x ≠ 3 x - 3 m k h i x = 3 . Tìm giá trị của m để hàm số liên tục tại x=3?
A. 
.
B. 
.
C. 
.
D. 
.
Chọn B
Tập xác định của hàm số là 
.
Ta có: 
.
.
Hàm số liên tục tại 
khi
Đúng 0
Bình luận (0)
Với giá trị nào của m thì hàm số y = x 3 - 6 x 2 + 9 x + m có giá trị lớn nhất trên [0;2] bằng -4
A. m=-8
B. m=-4
C. m=0
D. m=10
1 tháng 1 2024 lúc 17:48
Bài 5; Tìm x
a) x2-4=0
b) 2x(x+5)-3(5+x)=0
c) x3-6x2+11x-6=0
a) x² - 4 = 0
x² = 4
x = 2 hoặc x = -2
b) 2x(x + 5) - 3(5 + x) = 0
(x + 5)(2x - 3) = 0
X + 5 = 0 hoặc 2x - 3 = 0
*) x + 5 = 0
x = -5
*) 2x - 3 = 0
2x = 3
x = 3/2
c) x³ - 6x² + 11x - 6 = 0
x³ - x² - 5x² + 5x + 6x - 6 = 0
(x³ - x²) - (5x² - 5x) + (6x - 6) = 0
x²(x - 1) - 5x(x - 1) + 6(x - 1) = 0
(x - 1)(x² - 5x + 6) = 0
(x - 1)(x² - 2x - 3x + 6) = 0
(x - 1)[(x² - 2x) - (3x - 6)] = 0
(x - 1)[x(x - 2) - 3(x - 2)] = 0
(x - 1)(x - 2)(x - 3) = 0
x - 1 = 0 hoặc x - 2 = 0 hoặc x - 3 = 0
*) x - 1 = 0
x = 1
*) x - 2 = 0
x = 2
*) x - 3 = 0
x = 3
Vậy x = 1; x = 2; x = 3
Đúng 2
Bình luận (0)
Tìm giá trị lớn nhất của B=\(\frac{x^2+11x-5}{x^2+x+1}\)
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
3
−
6
x
2
+
7
trên đoạn
1
;
5
.
Khi đó tổng
M
+
m
bằng: A.
−
18
B.
−
16
C.
−
11
D. ...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 − 6 x 2 + 7 trên đoạn 1 ; 5 . Khi đó tổng M + m bằng:
A. − 18
B. − 16
C. − 11
D. − 23
Đáp án D.
Phương pháp
Phương pháp tìm GTLN, GTNN của hàm số y = f x trên [ a ; b ] .
+) Giải phương trình y ' = 0 ⇒ các nghiệm x i ∈ a ; b
+) Tính các giá trị f a ; f b ; f x i
+) So sánh và kết luận:
max a ; b f x = max f a ; f b ; f x i ; min a ; b f x = min f a ; f b ; f x i
Cách giải
Đúng 0
Bình luận (0)
Gọi M là giá trị lớn nhất của hàm số
f
(
x
)
6
x
2
-
6
x
+
12
+
6
x
-
x
2
-
4
. Tính tích các nghiệm của phương trình f(x)M. A. -6 B. 3 C. -3 D. 6
Đọc tiếp
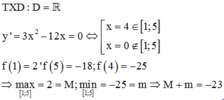
Gọi M là giá trị lớn nhất của hàm số f ( x ) = 6 x 2 - 6 x + 12 + 6 x - x 2 - 4 . Tính tích các nghiệm của phương trình f(x)=M.
A. -6
B. 3
C. -3
D. 6
Gọi M là giá trị lớn nhất của hàm số
f
(
x
)
6
x
2
-
6
x
+
12
+
6
x
-
x
2
-
4
. Tính tích các nghiệm của phương trình f(x) M. A. -6 B. 3 C. -3 D. 6
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số f ( x ) = 6 x 2 - 6 x + 12 + 6 x - x 2 - 4 . Tính tích các nghiệm của phương trình f(x) = M.
A. -6
B. 3
C. -3
D. 6
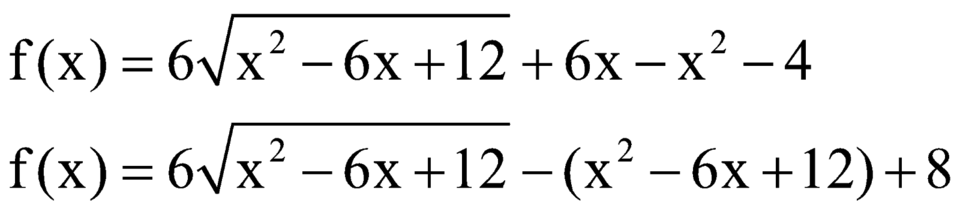
Đặt 
khi đó ta có 
Ta có 
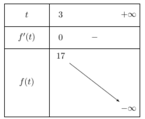
BBT:
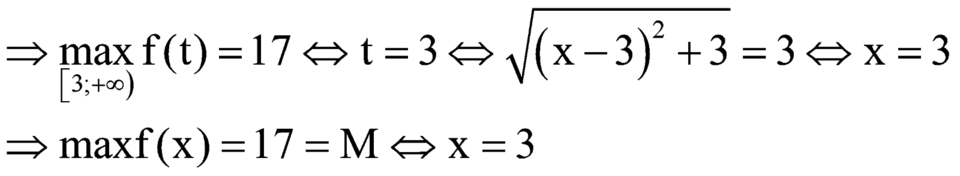
Vậy phương trình 
có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.
Chọn B
Đúng 0
Bình luận (0)
Bài 1: Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau:a) A a4-2a3+3a2-4a+5b) B dfrac{x^2+4x-6}{3}c) C dfrac{4+5left|1-2xright|}{7}Bài 2: a) Tìm a sao cho x4-x3+6x2-x+a chia hết cho đa thức x2-x+5.b) Xác định hằng số a và b sao cho x4+ax2+b chia hết cho x2-x+1Bài 3: Tính giá trị của biểu thức: A x17-12x14+...-12x12+12x-1 với x11
Đọc tiếp
Bài 1: Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau:
a) A= a4-2a3+3a2-4a+5
b) B= \(\dfrac{x^2+4x-6}{3}\)
c) C= \(\dfrac{4+5\left|1-2x\right|}{7}\)
Bài 2:
a) Tìm a sao cho x4-x3+6x2-x+a chia hết cho đa thức x2-x+5.
b) Xác định hằng số a và b sao cho x4+ax2+b chia hết cho x2-x+1
Bài 3: Tính giá trị của biểu thức: A= x17-12x14+...-12x12+12x-1 với x=11