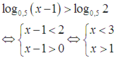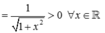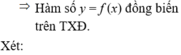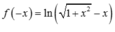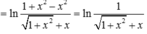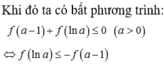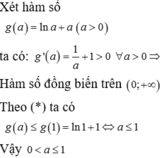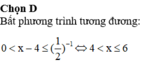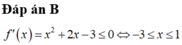Cho hàm số f(x) =log0,5(6x-x2). tập nghiệm của bất phương trình .

Những câu hỏi liên quan
Tập nghiệm của bất phương trình log0,5 (x - 1) log0,5 2 là:
Đọc tiếp
Tập nghiệm của bất phương trình log0,5 (x - 1) > log0,5 2 là:
![]()
![]()
![]()
![]()
Cho hàm số
f
(
x
)
l
n
(
x
2
-
2
x
+
3
)
. Tập nghiệm của bất phương trình f(x)0 là A.
(
2
;
+
∞
)
. B.
(
-
1
;
+
∞
)
. C.
(
-
2
;
+
∞
)...
Đọc tiếp
Cho hàm số f ( x ) = l n ( x 2 - 2 x + 3 ) . Tập nghiệm của bất phương trình f'(x)>0 là
A. ( 2 ; + ∞ ) .
B. ( - 1 ; + ∞ ) .
C. ( - 2 ; + ∞ ) .
D. ( 1 ; + ∞ ) .
Cho hàm số f ( x ) = 1 3 x 3 - x 2 + 2 x - 2009 . Tập nghiệm của bất phương trình f'(x) ≤ 0 là:
A. ∅
B. [-2;2]
C. 0 ; + ∞
D. R
Chọn A
- Ta có:
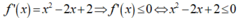
- Suy ra bất phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
ln
(
1
+
x
2
+
x
)
. Tập nghiệm của bất phương trình
f
(
a
-
1
)
+
f
(
ln
a
)
≤
0
là:
Đọc tiếp
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Tập nghiệm của bất phương trình
log
0
,
5
(
x
-
1
)
1
là A.
-
∞
;
3
2
B.
1
;
3
2
C. ...
Đọc tiếp
Tập nghiệm của bất phương trình log 0 , 5 ( x - 1 ) > 1 là
A. - ∞ ; 3 2
B. 1 ; 3 2
C. 3 2 ; + ∞
D. [ 1 ; 3 2 )
Cho hàm số
y
f
x
2
x
2
−
7
x
+
6
x...
Đọc tiếp
Cho hàm số y = f x = 2 x 2 − 7 x + 6 x − 2 k h i x < 2 a + 1 − x 2 + x k h i x ≥ 2 . Biết a là giá trị để hàm số f(x) liên tục tại x 0 = 2 , tìm nghiệm nguyên của bất phương trình − x 2 + a x + 7 4 > 0 .
A. 1
B. 4
C. 3
D. 2
Đáp án D
Ta có lim x → 2 − f x = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − − 2 x − 3 = − 1
Và lim x → 2 − f x = lim x → 2 − a + 1 − x 2 + x = a − 1 4 ; f 2 = a − 1 4 .
Theo bài ra, ta có lim x → 2 + f x = lim x → 2 − f x = f 2 ⇒ a = − 3 4
Do đó, bất phương trình − x 2 + a x + 7 4 > 0 ⇔ − x 2 − 3 4 x + 7 4 > 0 ⇔ − 7 4 < x < 1.
Đúng 0
Bình luận (0)
cho hàm số y=f(x)=x2. Tìm m để bất phương trình f(x-3)+5-m>0 cố tập nghiệm là R
\(f\left(x-3\right)+5-m>0\)
\(\Leftrightarrow\left(x-3\right)^2+5-m>0\)
\(\Leftrightarrow x^2-6x+14-m>0\)
BPT có tập nghiệm là R khi:
\(\Delta'=9-\left(14-m\right)< 0\)
\(\Leftrightarrow m< 5\)
Đúng 0
Bình luận (0)
Tập nghiệm bất phương trình:
l
o
g
0
,
5
(
x
−
4
)
+
1
≥
0
là: A.
4
;
9
2
B.
(
−
∞
;
6
)
C.
(
4
;
+...
Đọc tiếp
Tập nghiệm bất phương trình: l o g 0 , 5 ( x − 4 ) + 1 ≥ 0 là:
A. 4 ; 9 2
B. ( − ∞ ; 6 )
C. ( 4 ; + ∞ )
D. ( 4 ; 6 ]
Cho hàm số f(x)
1
3
x
3
+
x
2
-
3
x
+
1
. Tìm nghiệm của bất phương trình
f
(
x
)
≤
0
Đọc tiếp
Cho hàm số f(x) = 1 3 x 3 + x 2 - 3 x + 1 . Tìm nghiệm của bất phương trình f ' ( x ) ≤ 0
![]()
![]()
![]()
![]()
Cho hàm số
f
x
x
2
−
x
.
Tập nghiệm S của bất phương trình
f
x
≤
f
x
là: A.
S
−
∞
;
0
∪
2
+...
Đọc tiếp
Cho hàm số f x = x 2 − x . Tập nghiệm S của bất phương trình f ' x ≤ f x là:
A. S = − ∞ ; 0 ∪ 2 + 2 2 ; + ∞
B. S = − ∞ ; 0 ∪ 1 ; + ∞
C. S = − ∞ ; 2 − 2 2 ∪ 2 + 2 2 ; + ∞
D. S = − ∞ ; 2 − 2 2 ∪ 1 ; + ∞
Đáp án A
Tính f ' x sau đó giải bất phương trình.
TXĐ: D = − ∞ ; 0 ∪ 1 ; + ∞
Ta có f ' x = 2 x − 1 2 x 2 − x
f ' x ≤ f x ⇔ 2 x − 1 2 x 2 − x ≤ x 2 − x
DK: x ∈ − ∞ ; 0 ∪ 1 ; + ∞
⇔ 2 x − 1 2 x 2 − x − x 2 − x ≤ 0
⇔ 2 x − 1 − 2 x 2 − x ≤ 0 ⇔ 2 x + 4 x − 1 ≤ 0
⇔ x ∈ − ∞ ; 2 − 2 2 ∪ 2 + 2 2 ; + ∞
Kết hợp điều kiện ta có: x ∈ − ∞ ; 0 ∪ 2 + 2 2 ; + ∞
Đúng 0
Bình luận (0)