cho hàm số y=\(\frac{1}{3}\)x3+(m-2)x2 + (4m-1)x +3
a, tính y'
b.tìm m để hs có nghiệm
Cho hàm số y=(x-1)(x2+mx+m)
a. Với m=2, tính y', giải pt
b.Tìm m để tiếp tuyến tại điểm có hoành độ x=-1 song song với đường thẳng y=-2x-3
c. tìm m để pt y=0 có 3 nghiệm phân biệt x1,x2,x3 thỏa mãn x12 + x22 +x32 <4
d. tìm m để pt y=0 có 3 nghiệm phân biệt trong đó có 1 nghiệm lớn hơn 2
Số điểm cố định của đồ thị hàm số y = x 3 − 3 ( m + 1 ) x 2 + 2 ( m 2 + 4 m + 1 ) x − 4 m ( m + 1 ) khi m thay đổi là:
A. 0
B. 1
C. 2
D. 3
Đáp án B.
Gọi điểm cố định là A ( x 0 ; y 0 )
⇒ y 0 = x 0 3 − 3 ( m + 1 ) x 0 2 + 2 ( m 2 + 4 m + 1 ) x 0 − 4 m ( m + 1 ) ∀ m
⇔ 2 ( x 0 − 2 ) m 2 − ( 3 x 0 2 − 8 x 0 + 4 ) m + x 0 3 − 3 x o 2 + 2 x 0 − y 0 = 0 ∀ m
⇔ x 0 − 2 = 0 3 x 0 2 − 8 x 0 + 4 = 0 x 0 3 − 3 x 0 2 + 2 x 0 − y 0 = 0 ⇔ x 0 = 2 y 0 = 0 ⇒ A ( 2 ; 0 )
=>Có một điểm cố định
Số điểm cố định của đồ thị hàm số y = x 3 − 3 ( m + 1 ) x 2 + 2 ( m 2 + 4 m + 1 ) x − 4 m ( m + 1 ) khi m thay đổi là:
A. 0
B. 1
C. 2
D. 3
tìm m để hàm số y= X3 - (2m-3)X2 - (4m-15)x -5 có cực trị
y'=3x2-2(2m-3)x-(4m-15)
để hs y có cực trị thì y'=0 có 2 nghiệm phân biệt
Δ,=(2m-3)2-3(4m-15)>0
<=> 4m2-24m+54>0
<=>(2m-6)2+18>0 với mọi m
=> hs luôn có cực trị với mọi m
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
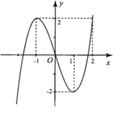
A.![]()
B. Với mọi m
C. ![]()
D. ![]()
Đáp án A
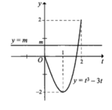
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()
Tìm m để các hàm số y = (m – 1)x3 – 3(m + 2)x2 – 6(m + 2)x + 1 có y’ ≥ 0, ∀ x ∈ R.
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. m ≥ 4 2
Tìm m để các hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 có y' ≥ 0 ∀x ∈ R
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. Không có giá trị nào thỏa mãn
- Ta có:
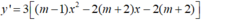
- Do đó:
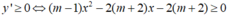 (1)
(1)
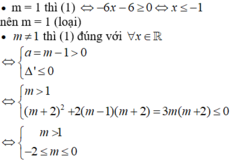
- Suy ra, không có giá trị nào của m thỏa mãn.
Chọn D.
Tìm m để các hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 có y ' ≥ 0 , ∀ x ∈ R
A. m ≥ 3
B. m ≥ 1
C. m ≥ 4
D. đáp án khác
Đáp án D
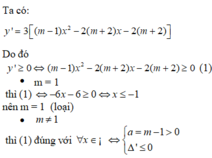
m > 1 m + 2 2 + 2 ( m − 1 ) . ( m + 2 ) = ( m + 2 ) .3 m ≤ 0 ⇔ m > 1 − 2 ≤ m ≤ 0 ⇔ ∃ m
Vậy không có giá trị nào của m thỏa mãn