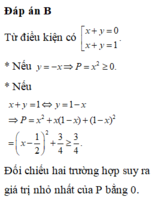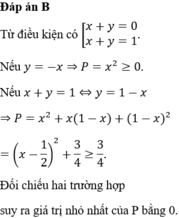Cho 2 số tự nhiên x,y thoả mãn 2x = 4.2y và 3x.3y = 81. Tính 2x + 3y

Những câu hỏi liên quan
cho x,y,z là các số dương thoả mãn \(\dfrac{1}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{z+x}\)=6
Chứng minh \(\dfrac{1}{3x+3y+2z}+\dfrac{1}{3x+2y+3z}+\dfrac{1}{2x+3y+3z}\)≤\(\dfrac{3}{2}\)
Áp dụng BĐT Cauchy-Schwarz:
\(\dfrac{1}{x+y}+\dfrac{1}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{z+x}\ge\dfrac{16}{3x+3y+2z}\\ \Leftrightarrow\dfrac{1}{3x+2y+2z}\le\dfrac{1}{16}\left(\dfrac{2}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{z+x}\right)\\ \Leftrightarrow\sum\dfrac{1}{3x+2y+2z}\le\dfrac{1}{16}\left(\dfrac{4}{x+y}+\dfrac{4}{y+z}+\dfrac{4}{z+x}\right)=\dfrac{4}{16}\cdot6=\dfrac{3}{2}\)
Dấu \("="\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Tìm các số tự nhiên x, y, z thỏa mãn (2x+y)2+3x+3y+1=z2
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức
P
x...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P = x 2 + x y + y 2 bằng
A. 3 4
B. 0
C. 1 4
D. 1 2
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức P
x
2
+
x
y...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P= x 2 + x y + y 2 bằng
A. 3 4
B. 0.
C. 1 4
D. 1 2
cho 2 số tự nhiên x và y thỏa mãn: 2x+1 . 3y = 12x khi đó x+y=?
Hỏi số dư của 1.2+1.2.3+1.2.3.4+1.2.3.4.5+⋯+1.2.3…99.100 khi chia cho 10 bằng bao nhiêu
Chữ số tận cùng của 7. 16^20.41^50
Cho hai số tự nhiên x,y thỏa mãn 2^x=4.2^y va 3^x.3^y=81. Tính 2x+3y
1 . 2 + 1 . 2 . 3 + 1 . 2 . 3 . 4 + 1 . 2 . 3 . 4 . 5 +⋯+ 1.2.3…99.100
1 x 2 + 1 x 2 x 3 + 1 x 2 x 3 x 4 + ... + 1 x 2 x 3 x ... x 99 x 100
chỉ có các số hạng sau là không có các số hạng sau ; 1 x 2 + 1 x 2 x 3 + 1 x 2 x 3 x 4 là không có tận cùng là 0 vì chúng không có các số dạng 5k
1 x 2 + 1 x 2 x 3 + 1 x 2 x 3 x 4 = 2 + 6 + 24 = 2 + 30
vì 30 \(⋮\)10 nhưng 2 \(⋮̸\)10 nên số dư của tông trên là 2
b) 7. 16^20.41^50
7 có tận cùng là 7
16^20 có tận cùng là 6 vì 6^20 = 6 x 6 x 6 ... x 6= 36 x 6 x ... x 6 luôn luôn có tận cùng là 6
41^50 có tận cung là 1 vì 41 có tận cùng là 1
Chữ số tận cùng của 7. 16^20.41^50 là : 7 x 6 x 1 = 42 chữ số tận cùng là 2
c) 2^x=4.2^y va 3^x.3^y=81. Tính 2x+3y
2^x = 4 x 2^y = 2^2 x 2^y = 2^2+y
3^x . 3^y = 81 = 3^4
vì 2^x = 2^y + 2 nên x = y + 2 mà x + y = 4 nên x = (4 + 2) : 2 = 3 y = 4 - 3 = 1
2x + 3y = 2 . 3 + 3 x 1 = 6 + 3 = 9
jniujreiuwrjrejhroirrijgbkjdyfnro9rkworeiuoooooijkrwlckkzajdaokopqkoswjigjwpskhpe[prtohposjiowejgfoKJPOHQWPODFGT0-654PATPJYIOEUEHWKS,EF TOOPN 5ROAE0294IRE;J,LH'PTO5RMGE9DC0DEPTHIJGM,F.RT[IKU,H.G'FD
SYLUJYUG;V/B';LT'FGDL,KOITHY0-P[TLIOTRP-RE[POTLE;J,TYF,VTY7I[EPTYH-=PE3-0RK0YBPOFLKJFJROIYIYPGYJO
Tìm các số tự nhiên x,y thoả mãn : 10 < x ; y < 30 và x = ƯCLN(2y+5; 3y + 2)
Do x=ƯCLN(2y+5;3y+2) nên ta có:
Đúng 1
Bình luận (0)
a) Cho các số thực dương x, y thoả mãn y ^ 2 + 2xy >= 29 - 4x chứng minh rằng 2x + 3y + 4/x + 18/y >= 21
Từ giả thiết:
\(29\le y^2+2xy+4x\le y^2+2xy+x^2+4\)
\(\Rightarrow\left(x+y\right)^2\ge25\Rightarrow x+y\ge5\)
Đặt \(P=2x+3y+\dfrac{4}{x}+\dfrac{18}{y}\)
\(\Rightarrow P=x+y+\left(x+\dfrac{4}{x}\right)+2\left(y+\dfrac{9}{y}\right)\ge5+2\sqrt{\dfrac{4x}{x}}+2.2\sqrt{\dfrac{9y}{y}}=21\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(2;3\right)\)
Đúng 0
Bình luận (0)
cho 2 số tự nhiên x và y thoả mãn 2x+3y=10 . giá trị của biểu thức B = 4x + 6y - 20 là
A. 0 B.10 C. 20 D.30
ta có B=4x+6y-20
=2(2x+3y)-20
do 2x+3y=10\(\Rightarrow\)B=2.10-20
\(\Rightarrow\)B=0
Đúng 0
Bình luận (0)