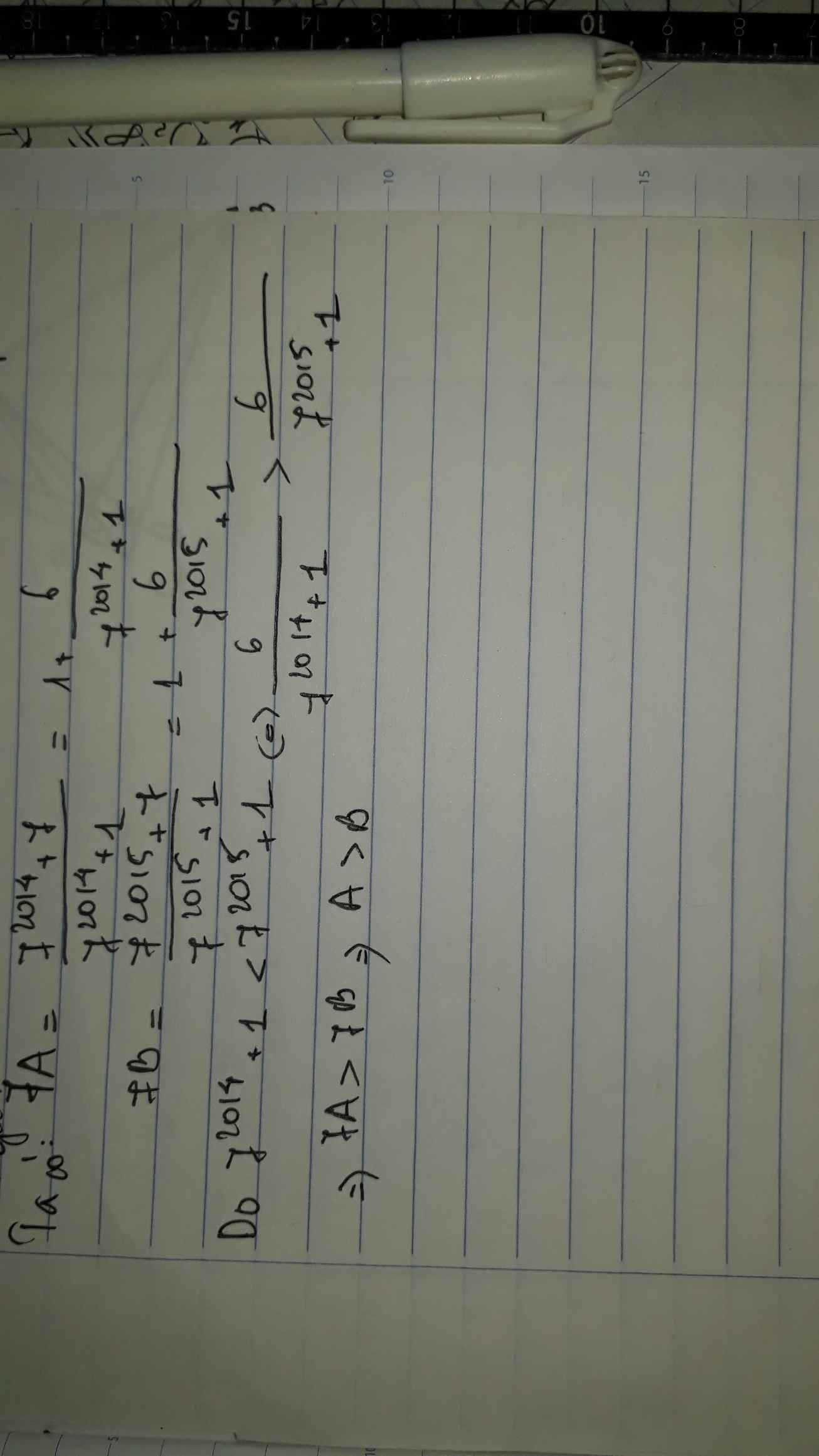SO SÁNH \(A=\frac{7^{2013}+1}{7^{2014}+1}\)VÀ \(B=\frac{7^{2014}+1}{7^{2015}+1}\)

Những câu hỏi liên quan
SO SÁNH: A=\(\frac{7^{2013}+1}{7^{2014}+1}\) B=\(\frac{7^{2014}+1}{7^{2015}+1}\)
HELP ME
\(\frac{^{^{2015^{2013}+1}}}{2015^{2014}+7}\)và \(\frac{2015^{2014}-2}{2015^{2015}-2}\)hãy so sánh 2 phân số đó
Đặt A= 2015^2013+1/2015^2014+7, B=2015^2014-2/2015^2015-2
2015A= 2015^2014+2015/2015^2014+7= 1 + (2008/2015^2014+7)
2015B= 2015^2015-4030/2015^2015-2= 1 - (4028/2015^2015-2)
Do 2015A>1>2015B nên A>B
Đúng 0
Bình luận (0)
Cho A= \(\frac{4+\frac{4}{2012}-\frac{4}{2013}+\frac{4}{2014}-\frac{4}{2015}}{\frac{7}{2014}-\frac{7}{2015}+\frac{7}{2012}-\frac{7}{2013}+7}\)
Và B= \(\frac{1+2+2^2+...+2^{2013}}{2^{2015}-2}\)
Tính A - B
p/S: LM ƠN GIÚP TỚ VS :
\(TA-CO':\)
\(A=\frac{4+\frac{7}{2014}-\frac{7}{2015}+\frac{7}{2012}-\frac{7}{2013}}{7+\frac{7}{2014}-\frac{7}{2015}+\frac{7}{2012}-\frac{7}{2013}}\)
\(A=\frac{4\left(\frac{1}{2014}-\frac{1}{2015}+\frac{1}{2012}-\frac{1}{2013}\right)}{7\left(\frac{1}{2014}-\frac{1}{2015}+\frac{1}{2012}-\frac{1}{2013}\right)}\)
\(A=\frac{4}{7}\)
\(B=\frac{1+2+...+2^{2013}}{2^{2015}-2}\)
ĐẶT \(C=1+2+...+2^{2013}\)
\(\Rightarrow2C=2+2^2+...+2^{2014}\)
\(\Rightarrow2C-C=\left(2+2^2+...+2^{2014}\right)-\left(1+2+...+2^{2013}\right)\)
\(\Rightarrow C=2^{2014}-2\)
\(\Rightarrow B=\frac{2^{2014}-1}{2^{2015}-2}\)
\(B=\frac{2^{2014}-1}{2\left(2^{2014}-1\right)}\)
\(B=\frac{1}{2}\)
\(\Rightarrow A-B=\frac{3}{7}-\frac{1}{2}=\frac{6}{14}-\frac{7}{14}\)
\(A-B=\frac{6-7}{14}=\frac{-1}{14}\)
VẬY, \(A-B=\frac{-1}{14}\)
Đúng 0
Bình luận (0)
So sánh:
a) A=9^10 và B= ( 8^9+7^9+6^9+...+2^9+1^9)
b) P= 2013/2014 + 2014/2015 + 2015/2016 với Q= 2013+2014+2015 / 2014+2015+2016
Câu 1: so sánh
A = \(\dfrac{7^{2013}+1}{7^{2014}+1}\) và B = \(\dfrac{7^{2014}+1}{7^{2015}+1}\)
Tham khảo: https://hoc24.vn/cau-hoi/so-sanh-afrac720131720141va-bfrac720141720151.235038064198
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
so sanh \(a=\frac{2013}{2014}+\frac{2014}{2015}\) va \(b=\frac{2013+2014}{2014+2015}\)
\(\frac{3}{x+1}
a = \(\frac{2013}{2014}+\frac{2014}{2015}=\frac{2014-1}{2014}+\frac{2015-1}{2015}\)
\(=1-\frac{1}{2014}+1-\frac{1}{2015}\)
\(=2-\left(\frac{1}{2014}+\frac{1}{2015}\right)>1\) (1)
b = \(\frac{2013+2014}{2014+2015}
Đúng 0
Bình luận (0)
havsvsuvsvsjzbsvshshsvshjsvdhsjvdhsjdvdhdjdhdhsjdhdhsudghsushdhshshgdgshshdgshdhshdhdghshdgdvshhshdvdgdhshgdgd
h
Đúng 0
Bình luận (0)
1/Cho a;b;cinN*. Chứng minh :Nếu frac{a}{b}1thì frac{a}{b}frac{a+c}{b+c}2/Từ bài trên,so sánha)frac{2014^{2013}+1}{2014^{2014}+1}và frac{2014^{2012}+1}{2014^{2013}+1}b)frac{7^{58}+2}{7^{57}+2}và frac{7^{57}+2009}{7^{56}+2009}
Đọc tiếp
1/Cho a;b;c\(\in\)N*. Chứng minh :Nếu \(\frac{a}{b}<1\)thì \(\frac{a}{b}<\frac{a+c}{b+c}\)
2/Từ bài trên,so sánh
a)\(\frac{2014^{2013}+1}{2014^{2014}+1}\)và \(\frac{2014^{2012}+1}{2014^{2013}+1}\)
b)\(\frac{7^{58}+2}{7^{57}+2}\)và \(\frac{7^{57}+2009}{7^{56}+2009}\)
ồ thú vị đấy mình học rồi nhưng busy thông cảm ha^_^
Đúng 0
Bình luận (0)
ngoài ra a/b>1 thì a+m/b+m > 1 (m thuộc z, m khác 0) và a,b cậu biết rồi đó
Đúng 0
Bình luận (0)
\(\frac{a}{b}=\frac{ab+ac}{b\left(b+c\right)};\frac{a+c}{b+c}=\frac{ab+bc}{b\left(b+c\right)}\Rightarrow ab+bc>ab+ac\left(\frac{a}{b}< 1\right)\Rightarrow dpcm\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
So sánh A=\(\frac{2014^{2015}+1}{2014^{2015}+1}\) va B=\(\frac{2014^{2014}+1}{2014^{2013}+1}\)
Ta có :
\(\frac{2014^{2015}+1}{2014^{2015}+1}\)\(=1\)
\(\frac{2014^{2014}+1}{2014^{2013}+1}\)\(>1\)
\(\Rightarrow A< B\)
Vậy \(A< B\)
Đúng 1
Bình luận (0)
cho A=\(\frac{7^{2011}+1}{7^{2013}+1}\)và B=\(\frac{7^{2013}+1}{7^{2015}+1}\)HÃY SO SÁNH A VÀ B