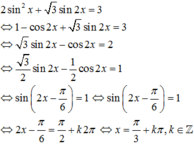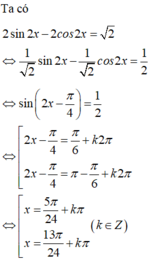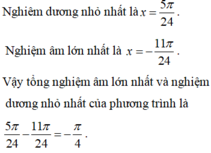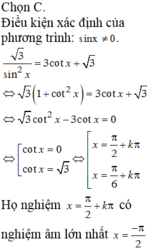phương trình sau có nghiệm 2sin²2x+√3sin2x=3

Những câu hỏi liên quan
Bài 1: Tìm nghiệm âm lớn nhất
-2Sin22x + 3Sin2x=0
Bài 2: Tìm số nghiệm của phương trình
Sin(2x + pi/3) = -căn bậc 2 của 3/ 2
1. Tập hợp tất cả các nghiệm thuộc [-pi;pi] của pt 2sin^2x + 2sin2x=3-3cos^2x là
2. Phương trình 2cos^x-3√3sin2x-4sin^2=-4 có số nghiệm thuộc (0;2pi) là ?
Giúp mik/em với ạ
1.
\(2sin^2x+4sinx.cosx=3-3cos^2x\)
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^2x\)
\(\Rightarrow2tan^2x+4tanx=3\left(1+tan^2x\right)-3\)
\(\Leftrightarrow2tan^2x+4tanx=3tan^2x\)
\(\Leftrightarrow tan^2x-4tanx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=0\\tanx=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=arctan\left(4\right)+k\pi\end{matrix}\right.\)
Các nghiệm thỏa mãn là: \(\left\{-\pi;0;\pi;arctan\left(4\right)-\pi;arctan\left(4\right)\right\}\)
Có 5 nghiệm trên đoạn đã cho
Đúng 0
Bình luận (0)
2.
Chắc đề là \(2cos^2x-3\sqrt{3}sin2x-4sin^2x=-4\)
\(\Leftrightarrow2cos^2x-6\sqrt{3}sinx.cosx+4\left(1-sin^2x\right)=0\)
\(\Leftrightarrow2cos^2x-6\sqrt{3}sinx.cosx+4cos^2x=0\)
\(\Leftrightarrow6cos^2x-6\sqrt{3}sinx.cosx=0\)
\(\Leftrightarrow6cosx\left(cosx-\sqrt{3}sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\tanx=\frac{1}{\sqrt{3}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{6}+k\pi\end{matrix}\right.\)
Các nghiệm thuộc đoạn đã cho: \(\left\{\frac{\pi}{2};\frac{3\pi}{2};\frac{\pi}{6};\frac{7\pi}{6}\right\}\) có 4 nghiệm thỏa mãn
Đúng 0
Bình luận (0)
Phương trình
2
sin
2
x
+
3
sin
2
x
3
có nghiệm là A.
x
π
3
+
k
π
,
k
∈
ℤ
B.
x
2
π
3
+
k
π
,
k
∈...
Đọc tiếp
Phương trình 2 sin 2 x + 3 sin 2 x = 3 có nghiệm là
A. x = π 3 + k π , k ∈ ℤ
B. x = 2 π 3 + k π , k ∈ ℤ
C. x = 4 π 3 + k π , k ∈ ℤ
D. x = 5 π 3 + k π , k ∈ ℤ
Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
2
sin
2
x
-
2
cos
2
x
2
bằng: A. 0 B.
π
4
C.
-
3
π
4
D.
-
π
4
Đọc tiếp
Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 2 sin 2 x - 2 cos 2 x = 2 bằng:
A. 0
B. π 4
C. - 3 π 4
D. - π 4
Chọn D.
Phương pháp: Giải phương trình và tìm nghiệm âm lớn nhất, nghiệm dương nhỏ nhất.
Cách giải: Ta có:
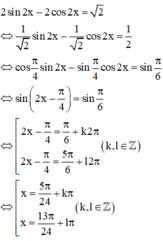
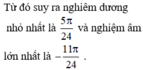
Vậy tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
2
sin
2
x
-
2
cos
2
x
=
2
![]()
Đúng 0
Bình luận (0)
Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình bằng 2sin 2x-2cos 2x
2
A. 0 B.
π
4
C.
-
3
π
4
D.
-
π
4
Đọc tiếp
Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình bằng 2sin 2x-2cos 2x = 2
A. 0
B. π 4
C. - 3 π 4
D. - π 4
Phương trình
3
sin
2
x
-
cos
2
x
2
có tập nghiệm
Đọc tiếp
Phương trình 3 sin 2 x - cos 2 x = 2 có tập nghiệm
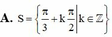
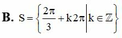


Phương trình 3 sin 2 x + m sin 2 x – 4 cos 2 x = 0 có nghiệm khi:
A. m = 4
B. m ≥ 4
C. m ≤ 4
D. m ∈R
giải phương trình sau:
\(2sin^2x+\sqrt{3}sin2x=3\)
`2sin^2x+\sqrt3sin2x=3`
`<=>2. (1-cos2x)/2 + \sqrt3sin2x=3`
`<=>\sqrt3sin2x-cos2x=2`
`<=> \sqrt3/2 sin2x-1/2 cos2x=1`
`<=>sin (2x-π/6) = 1`
`<=> 2x-π/6=π/2+k2π`
`<=> x=π/3+kπ (k \in ZZ)`.
Đúng 1
Bình luận (0)
\(\Leftrightarrow1-cos2x+\sqrt{3}sin2x=3\)
\(\Leftrightarrow\sqrt{3}sin2x-cos2x=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
Đúng 1
Bình luận (0)
Nghiệm âm lớn nhất của phương trình
3
sin
2
x
3
c
o
t
x
+
3
A.
-
π
6
B.
-
5
π
6
C.
-
π...
Đọc tiếp
Nghiệm âm lớn nhất của phương trình 3 sin 2 x = 3 c o t x + 3
A. - π 6
B. - 5 π 6
C. - π 2
D. - 2 π 3