tìm số nguyên tố a,b,c thoả mãn abc<ab+bc+ac

Những câu hỏi liên quan
tìm các số nguyên tố a;b;c thoả mãn a^2+c^2=abc
giả sử 1 trong 3 số=2
=>abc chia hết cho 2
=>a;c chia hết cho 2
=>a=c=2=>b=2
với a;b;c cùng lẻ=>a^2+c^2 chia hết cho 2
mà abc ko chia hết cho 2=>vô lí
Vậy a=b=c=2
Đúng 0
Bình luận (0)
2. Tìm các số tự nhiên n thoả mãn n2 +3n+2 là số nguyên tố.
3. Tìm các số tự nhiên n sao cho 2n +34 là số chính phương.
4. Chứng minh rằng tổng S = 14 +24 +34 +···+1004 không là số chính phương.
5. Tìm các số nguyên dương a ≤ b ≤ c thoả mãn abc,a+b+c,a+b+c+2 đều là các số nguyên tố
Mik gấp
đặt 2n + 34 = a^2
34 = a^2-n^2
34=(a-n)(a+n)
a-n thuộc ước của 34 là { 1; 2; 17; 34} và a-n . Ta có bảng sau ( mik ko bt vẽ)
=> a-n 1 2
a+n 34 17
Mà tổng và hiệu 2 số nguyên cùng tính chẵn lẻ
Vậy ....
Đúng 1
Bình luận (0)
Ta cóS = 14 +24 +34 +···+1004 không là số chính phương.
=> S= (1004+14).100:2=50 900 ko là SCP
Đúng 1
Bình luận (0)
2: A=n^2+3n+2=(n+1)(n+2)
Để A là số nguyên tố thì n+1=1 hoặc n+2=2
=>n=0
Đúng 0
Bình luận (0)
tìm bộ ba số nguyên tố a, b, c thoả mãn : a^c-b, c^a+b đều là số nguyên tố
tìm 3 số nguyên tố liên tiếp a,b,c(a<b<c) thoả mãn A=a^2+b^2+c^2 là số nguyên tố
tìm các số nguyên tố a,b,c thoả mãn điều kiện a.b.c=3(a+b+c)
Tìm các số nguyên tố a,b, c thoả mãn
\(a^2+b^2+6c^2=4abc\)
Tìm các số nguyên dương a, b, c đôi một nguyên tố cùng nhau thoả mãn:
1/a + 1/b = 1/c
Tìm các số nguyên tố a, b, c thoả món điiêù kiện abc = 3(a + b + c)
Từ abc = 3(a + b + c) suy ra a chia hết cho 3 hoạc b chia hết cho 3 hoặc c chia hết cho 3. Vậy
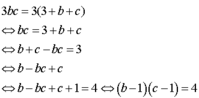
Do b và c là các sốnguyên tố b - 1 ≥ 1 ; c - 1 ≥ 1 và b – 1 , c – 1 là ước của 4 vậy chúng nhận 1 trông các giá trị là 1, 2, 4. Vậy ta có các trường hợp sau:
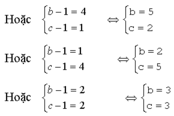
Các cặp số (a, b, c) phải Tìm là : (3, 3, 3) ; (3, 2, 5) ; (3, 5, 2) ; (5, 3, 2 ) ; (5, 2, 3) ; (2, 3, 5) ; (2, 5, 3)
Đúng 0
Bình luận (0)
a) Tìm số nguyên tố p thoả mãn \(2^p+1⋮p\)
b) Chứng minh rằng không có số tự nhiên n nào thoả mãn \(2^n+1⋮7\)
a. Ta có: \(2^p+1=\left(2^p-2\right)+3\)
Mà theo định lý Ferma nhỏ: \(2^p-2⋮p\Rightarrow3⋮p\Rightarrow p=3\)
b.
- Với \(n=3k\Rightarrow2^n+1=2^{3k}+1=8^k+1\)
Mà \(8\equiv1\left(mod7\right)\Rightarrow8^k+1\equiv2\left(mod7\right)\Rightarrow\) ko chia hết cho 7
- Với \(n=3k+1\Rightarrow2^n+1=2^{3k+1}+1=2.8^k+1\)
\(2.8^k+1\equiv3\left(mod7\right)\Rightarrow\) ko chia hết cho 7
- Với \(n=3k+2\Rightarrow2^n+1=2^{3k+2}+1=4.8^k+1\)
\(4.8^k+1\equiv5\left(mod7\right)\Rightarrow\) không chia hết cho 7
Vậy \(2^n+1\) ko chia hết cho 7 với mọi n
Đúng 1
Bình luận (0)


















