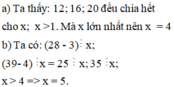Đây là toán nâng cao chuyên đề lập số theo điều kiện cho trước, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

                                   Giải:

Vì 13; 15; 61 chia \(x\) đều dư 1 nên 13; 15; 61 khi đồng thời bớt đi 1 sẽ trở thành số chia hết cho \(x\)

Từ lập luận trên ta có:

           \(\left\{{}\begin{matrix}13-1⋮x\\15-1⋮x\\61-1⋮x\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}12⋮x\\14⋮x\\60⋮x\end{matrix}\right.\) ⇒ \(x\) \(\in\) ƯC(12; 14; 60)

Mà \(x\) lại là số tự nhiên lớn nhất nên \(x\in\) ƯCLN(12; 14; 60)

12 = 2².3; 14 = 2.7; 60 = 2².3.5

ƯCLN(12; 14; 60) = 2 

Vậy \(x=2\)

13 chia x dư 1 suy ra 12 chia hết cho x

15 chia x dư 1 suy ra 14 chia hết cho x

61 chia x dư 1 suy ra 60 chia hết cho x

x thuộc ƯCLN(12,14,60) suy ra x=2

chúc bạn hok tốt :>

                                                            Bài giải         

Gọi số tự nhiên cần tìm là;a,(a\(\in\)N,a>1)

Ta có:\(\hept{\begin{cases}13:a\\15:a\\60:a\end{cases}}Dư1\)\(\Rightarrow\)\(\hept{\begin{cases}13-1⋮a\\15-1⋮a\\61-1⋮a\end{cases}}\)\(\Rightarrow\)\(\hept{\begin{cases}12⋮a\\14⋮a\\60⋮a\end{cases}}\)

\(\Rightarrow a\inƯC\left(12,14,60\right)\)mà a lớn nhất

\(\Rightarrow a\inƯCLN\left(12,14,60\right)\)

\(12=2^2.3\)          \(14=2.7\)                \(60=2^2.3.5\)

\(\RightarrowƯCLN\left(12,14,60\right)=2\)

\(\Rightarrow a=2\)

Vậy số tự nhiên cần tìm là:2

 1/

12 , 14 , 60 chia hết cho a

mà số lớn nhất thỏa mãn yêu cầu là 2

vì chia hết cho 12 chỉ có : 1 , 2 , 3 , 4 , 6 , 12

 14 là : 1 , 2 , 7 , 14

vậy a lớn nhất là 2

2/

42 , 84 , 63 chia hết cho a

a = 3

vì chia hết cho 63 có : 1 , 3 , 9 , ...

42 : 1 , 3 , 6 , 7 , 2 , ....

vì vậy a lớn nhất = 3

3)1;4;9;16;25;36;...
4)1;2;3;4;7;11;18;...
5)1;2;5;9;16;27;...
6)0;3;8;15;24;35;...
7)2;5;10;17;26;...
8)1;3;6;10;15;21;28;...

a) Vì 13, 15,61 chia cho a đều dư 1 => 13;15;61 \(⋮a-1\) 

=> a-1 thuộc ƯC(13;15;61)

Mà a lớn nhất => a-1 thuộc ƯCLN(13,15,61) 

Mà 13;15;61 là các số nguyên tố cùng nhau => ƯCLN(13;15;61) = 1

=> a-1=1

=>a=2

Vậy a=2.

b) Ta có: 149 : a dư 29 => (149-29) thì chia hết cho a ( a > 29)

                235 : a dư 35 => ( 235 -  35) chia hết cho a ( a> 35)

=> a thuộc ƯCLN(120,200) = 40

=> a = 40

Vậy a = 40

c) câu c tương tự câu b

a chia cho 4, 5, 6 dư 1

nên (a - 1) chia hết cho 4, 5, 6 

=> (a - 1) là bội chung của (4,5,6)

=> a - 1 = 60n 

=> a = 60n+1 

với 1 ≤ n < (400-1)/60 = 6,65 mặt khác a chia hết cho 7 

=> a = 7m 

Vậy 7m = 60n + 1 có 1 chia 7 dư 1

=> 60n chia 7 dư 6 mà 60 chia 7 dư 4 

=> n chia 7 dư 5 mà n chỉ lấy từ 1 đến 6 

=> n = 5 a = 60.5 + 1 = 301 

13;15;61 đều chia a dư 1 => 12;14;60 đều chia hết cho a

12 = 2² . 3

14 = 2 . 7

60 = 2² . 3 . 5

ƯCLN ( 12, 14, 60 ) = 2 

Vậy a = 2

ahihi  a=2 nha

1, Gọi số đó là :a

=>a-3⋮4,6,8

=>a-3 ϵ\(\left\{24,48,72,96,120,...\right\}\)

=>a ϵ\(\left\{27,51,75,99,123,...\right\}\)

Vì a là số nhỏ nhất có 3 chữ số thỏa mãn đề bài nên a=123.

Tìm kiếm bài học, bài tập, mã lớp, mã khóa học...

hehe

a = 2 nha bạn 

a chia cho 4, 5, 6 dư 1

nên (a - 1) chia hết cho 4, 5, 6 

=> (a - 1) là bội chung của (4,5,6)

=> a - 1 = 60n 

=> a = 60n+1 

với 1 ≤ n < (400-1)/60 = 6,65 mặt khác a chia hết cho 7 

=> a = 7m 

Vậy 7m = 60n + 1 có 1 chia 7 dư 1

=> 60n chia 7 dư 6 mà 60 chia 7 dư 4 

=> n chia 7 dư 5 mà n chỉ lấy từ 1 đến 6 

=> n = 5 a = 60.5 + 1 = 301