Ví dụ về hình trụ, hình nón, hình cầu

Những câu hỏi liên quan
- Thế nào là một mặt tròn xoay? Tìm trong thực tế một ví dụ về mặt tròn xoay.
- Định nghĩa hình nón, hình trụ. Trong thực tế một ví dụ về hình nón, hình trụ
- Trong mặt phẳng (P) cho hai đường thẳng Δ và l song song với nhau, cách nhau một khoảng bằng r. Khi quay mặt phẳng (P) xung quanh trục Δ thì đường thẳng l sinh ra một mặt tròn xoay gọi là mặt trụ tròn xoay và được gọi tắt là mặt trụ.
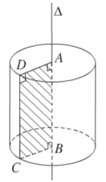
- Hình trụ là hình giới bạn bởi mặt trụ và hai đường tròn bằng nhau, là giao tuyến của mặt trụ và 2 mặt phẳng vuông góc với trục.
Hình trụ là hình tròn xoay khi sinh bởi bốn cạnh của hình một hình chữ nhật khi quay xung quanh một đường trung bình của hình chữ nhật đó.
- Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.
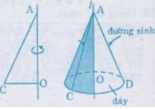
+ Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.
+ Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .
+ A là đỉnh và AO là đường cao của hình nón.


Đúng 0
Bình luận (0)
Câu 1: Hình chiếu ? các phép chiếu? Tên gọi hình chiếu ?Vị trí các hình chiếu trên bản vẽ kĩ thuật ?Câu 2: Khái niệm ,hình chiếu, ví dụ hình hộp chữ nhật , lăng trụ đều, hình chóp đều ?Câu 3 : Khối tròn xoay : Hình trụ, hình nón, hình cầu cách tạo thành ? Hình chiếu ? (hình dạng , tên hình chiếu, kích thước ) ?Câu 4:Nếu đặt mặt đáycủa hình trụ song song với mặt phẳng chiếu cạnh, thì hình chiếu đứng , bằng, cạnh có hình dạng như thế nào ?Câu 5: Nếu đặt mặt đáycủa hình nón song song với mặt phẳng...
Đọc tiếp
Câu 1: Hình chiếu ? các phép chiếu? Tên gọi hình chiếu ?Vị trí các hình chiếu trên bản vẽ kĩ thuật ?
Câu 2: Khái niệm ,hình chiếu, ví dụ hình hộp chữ nhật , lăng trụ đều, hình chóp đều ?
Câu 3 : Khối tròn xoay : Hình trụ, hình nón, hình cầu cách tạo thành ? Hình chiếu ? (hình dạng , tên hình chiếu, kích thước ) ?
Câu 4:Nếu đặt mặt đáycủa hình trụ song song với mặt phẳng chiếu cạnh, thì hình chiếu đứng , bằng, cạnh có hình dạng như thế nào ?
Câu 5: Nếu đặt mặt đáycủa hình nón song song với mặt phẳng chiếu cạnh, thì hình chiếu đứng , bằng, cạnh có hình dạng như thế nào ?
Câu 6 : Khái niệm hình cắt ? Hình cắt dùng làm gì ?
Câu 7: Nội dung, tình tự đọc bản vẽ chi tiết ?
Câu 8: Nội dung, trình tự bản vẽ lắp ?
Câu 9 : Chi tiết có ren, quy ước vẽ ren ?
ví dụ hình trụ,hình cầu?
Lấy ví dụ về hình nón giùm mình với, mình đang cần gấppp
+Kim tự tháp
+đầu tên lửa
+ nón lá
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho ví dụ về hình hộp chữ nhật, hình lăng trụ đều, hình chóp đều trong thực tế?
Một hình cầu nội tiếp trong một hình nón tròn xoay. Một hình trụ ngoại tiếp hình cầu đó và có đáy dưới nằm trong mặt phẳng đáy của hình nón. Gọi V1, V2 lần lượt là thể tích của khối nón và khối trụ. Giá trị nhỏ nhất của của
V
1
V
2
là
A
.
1
3
B
.
3
7...
Đọc tiếp
Một hình cầu nội tiếp trong một hình nón tròn xoay. Một hình trụ ngoại tiếp hình cầu đó và có đáy dưới nằm trong mặt phẳng đáy của hình nón. Gọi V1, V2 lần lượt là thể tích của khối nón và khối trụ. Giá trị nhỏ nhất của của V 1 V 2 là

A . 1 3
B . 3 7
C . 4 3
D . 7 3
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một nón tròn xoay (N) có góc ở đỉnh bằng
60
°
. Tính tỉ số thể tích của hình trụ (T) và hình nón (N).
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (T) và hình nón (N).
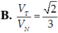
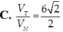
![]()
hình nón, hình trụ, chóp đều , hộp chữ nhật , lăng trụ đều, cầu là hình như thế nào
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng
60
°
. Tính tỉ số thể tích của hình trụ (N) và hình nón (T). A.
V
T
V
N
2
6
B. ...
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (N) và hình nón (T).
A. V T V N = 2 6
B. V T V N = 2 3
C. V T V N = 3 2
D. Đáp án khác
Đáp án A.
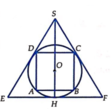
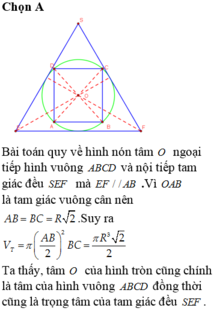
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ S E F đều” (hình vẽ).
Hình vuông ABCD nội tiếp đường tròn (O) nên
A B = B D = 2 R = A B 2 ⇔ A B = 2 R .
⇒ Bán kính đáy và chiều cao của hình trụ (T) lần lượt là r = A B 2 = 2 R 2 và h = A B = 2 R .
Thể tích khối trụ là V T = πr 2 h = π . 2 R 2 2 . 2 R = π 2 R 3 2 .
Ta có ∆ S E F đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của Δ S E F .
Gọi H là trung điểm của EF thì S H = 3 O H = 3 R ⇒ H F = S H . tan 30 ° = R 3
⇒ Bán kính đáy và chiều cao của hình nón (N) lần lượt là H F = R 3 và S H = 3 R . Thể tích khối nón là V N = 1 3 π . HF 2 . SH = 1 3 π R 3 2 . 3 R = 3 πR 3 .
Vậy V T V N = π 2 R 3 2 3 πR 3 = 2 6 .
Đúng 0
Bình luận (0)
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng
60
0
. Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A
.
V
T
V
N
2...
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 0 . Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A . V T V N = 2 6
B . V T V N = 2 3
C . V T V N = 3 2
D. Đáp án khác
Đáp án A.
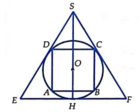
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ SEF đều” (hình vẽ).
![]()
=>Bán kính đáy và chiều cao của hình trụ (T) lần lượt là
![]()
và ![]()
Thể tích khối trụ là
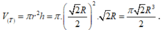
Ta có ∆ SEF đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của ∆ SEF.
Gọi H là trung điểm của EF thì
Hình vuông ABCD nội tiếp đường tròn (O) nên SH = 3OH = 3R![]()
Bán kính đáy và chiều cao của hình nón (N) lần lượt là ![]()
Thể tích khối nón là
![]()
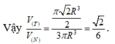
Đúng 0
Bình luận (0)