Áp dụng hệ thức lượng trong tam giác ABC vuông tại A

Ta có: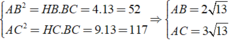

Vậy S A B C   =   1 2 A B . A C   =   1 2 . 2 13   . 3 13 =   39 c m 2

Chọn đáp án A.

a: \(AH=2\sqrt{6}\left(cm\right)\)

\(AB=2\sqrt{10}\left(cm\right)\)

\(AC=2\sqrt{15}\left(cm\right)\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{6}\left(cm\right)\\AC=2\sqrt{15}\left(cm\right)\\AB=2\sqrt{10}\left(cm\right)\end{matrix}\right.\)

Giải ra đi

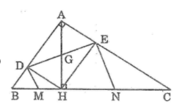
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật

Suy ra: AH = DE (tính chất hình chữ nhật)

Tam giác ABC vuông tại A và có AH là đường cao

Theo hệ thức giữa đường cao và hình chiếu ta có:

A H 2  = HB.HC = 4.9 = 36 ⇒ AH = 6 (cm)

Vậy DE = 6 (cm)

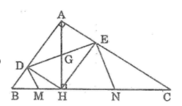
Tam giác BDH vuông tại D có DM là đường trung tuyến nên:

Chọn A

c: Xét ΔABM vuông tại A có AK là đường cao

nên \(BK\cdot BM=AB^2\left(1\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(BH\cdot BC=AB^2\left(2\right)\)

Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

a: BC=BH+CH

=4+6

=10(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>\(AH=\sqrt{4\cdot6}=2\sqrt{6}\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}AB=\sqrt{4\cdot10}=2\sqrt{10}\left(cm\right)\\AC=\sqrt{6\cdot10}=2\sqrt{15}\left(cm\right)\end{matrix}\right.\)

b: M là trung điểm của AC

=>\(AM=\dfrac{AC}{2}=\sqrt{15}\left(cm\right)\)

Xét ΔAMB vuông tại A có

\(tanAMB=\dfrac{AB}{AM}=\sqrt{\dfrac{2}{3}}\)

=>\(\widehat{AMB}\simeq39^0\)

c: ΔABM vuông tại A có AK là đường cao

nên \(BK\cdot BM=BA^2\left(1\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AB^2=BH\cdot BC\left(2\right)\)

Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

  Hình vẽ đây!