Áp dụng hệ thức lượng trong tam giác ABC vuông tại A
Ta có: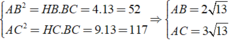
Vậy S A B C = 1 2 A B . A C = 1 2 . 2 13 . 3 13 = 39 c m 2
Chọn đáp án A.
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A
Ta có: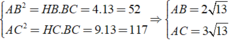
Vậy S A B C = 1 2 A B . A C = 1 2 . 2 13 . 3 13 = 39 c m 2
Chọn đáp án A.
Cho tam giác ABC vuông tại A, đường cao AH, phân giác góc B cắt AH tại I và cắt AC tại D. C/m:
a, tam giác HBA ddoognf dạng tam giác ABC
b, IH.DC=IA.AD
c, Giả sử phân giác AG của góc BAC chia cạnh huyền BC thành 2 đoạn có độ dài là 1 cm và 3cm ( G thuộc BC). TÍnh tỉ số BH trên HC
Mọi ng giúp mk nhé
Cho ![]() ABC vuông tại A có AH là đường cao.
ABC vuông tại A có AH là đường cao.
a/ Chứng minh: DABC đồng dạng DHAC
b/ Chứng minh: AC = HC.BC
c/ Tính tỉ số diện tích hai tam giác ABH và CBA, biết BH = 4cm, HC = 9cm.
d/ Gọi I là trung điểm của AH và K thuộc AB sao cho B là trung điểm của AK. Chứng minh: góc HIB = góc ACK
1.Cho tam giác ABC vuông tại A,biết AB=9cm,AC=12cm.Từ A kẻ đường cao AH xuống cạnh BC(đường cao vuông góc với đáy).
a) C/m tam giác ABC đồng dạng tam giác HAC.
b) C/m \(AC^2=BC.HC\)
c)Tính HC,BH và AH
2.Tính thể tích hình hộp chữ nhật.Biết \(S_{day}=12cm^2\)và chiều cao là 3cm.
cho tam giác ABC vuông tại A.Đường trung tuyến AH,đường cao AM.(H thuộc BC,M thuộc BC)
a)chứng minh tam giác ABH đồng dạng với tam giác ABC
b)chứng minh AH*AH=BH*CH
c)tính diện tích tam giác AMH biết BH=4cm,CH=9cm.
Cho Tam giác ABC vuông tại A ( AB < AC ) có đường cao AH
a) Chứng minh tam giác ABC đồng dạng tam giác CBA
b) Chứng minh AH2 = BH . HC
c) Trên đường thẳng vuông góc AC tại C , lấy điểm D sao cho CD = AB ( D và B nằm khác phía sao với đường thẳng AC ) . Đoạn thẳng HD cắt đoạn thẳng AC tại S . Kẻ AF vuông góc HS tại F .CM BH . CH = HF.HD
d) CM SFC = SHC
cho tam giác ABC vuông tại a đường cao AH a) chứng minh tam giác ABC ~ tam giác HBA từ đó suy ra AB^2=BH .BC b) cho BH=4cm CH=9cm tính AH,AB c) gọi F điểm tùy ý trên AC, đường thẳng qua H vuông góc HF cắt cạnh AB tại E chứng minh AE . CH=AH . FC d) xác định vị trí của F trên AC để đoạn FE có độ dài ngắn nhất
Cho tam giác ABC vuông tại A(AB<AC) đường cao AH, biết BH =9cm,HC =16cm.Gọi M là trung điểm của BC, đường vuông góc với BC tại M cắt AC ở D.
a, CM: tam giác MDC đồng dạng với tam giác ABC
b, CM: AH2=HB.HC
c, Tính MD
d, Gọi k là hình chiếu của M trên AC tính diện tích tam giác KDM
Cho tam giác ABC vuông tại A vẽ đường cao AH chia cạnh huyền BC thành hai đoạn thẳng BH=20cm và CH=45cm
a)Chứng minh tam giác HBA đồng dạng với tam giác HAC
b)Tính độ dài AH
c)Tính diện tích tam giác ABC
d)Cho AB=10 căn 3 ,AC=15 căn 3 .Gọi AD là đường phân giác trong của góc A và AH là đường cao .Tính tỉ số diện tích của tam giác ABC và tam giác ACD
Câu 1:Cho tam giác ABC vuông tại A (AC>AB) AH là đường cao. Từ trung điểm I của cạnh AC về ID vuông góc với cạnh huyền BC. Biết AB =3cm, AC=4cm
a) Tính độ dài cạnh BC
b) Cm: tam giác IDC đồng dạng tam giác BHA
Câu 2: Cho hình chữ nhật ABCD có AB=8cm, BC =6cm . Vẽ đường cao AH của tam giác ADB
a) Tính DB
b) Cm: tâm giác ADH đồng dạng tam giác ADB
c) Cm: AD^2=DH.DB
d) Cm: tâm giác AHB đồng dạng tam giác BCD
e) Tính độ dài đoạn thẳng DH,AH
Câu 3:Cho tam giác ABC vuông tại A có AB =6cm, AC =8cm .Vẽ đường cao AH
a) Tính BC
b) Cm : tam giác ABC đồng dạng tam giác AHB
c) Cm: AB^2=BH.BC.Tính BH, HC
d) Vẽ phân giác AD của góc A (D thuộc BC). Tính DB