Cho tam giác ABC, I là điểm di động trên đoạn BN, đặt x2 = IIB/ IIN, xx ## 0
a) CMR: vtAM=1/4 vtAB+3/4 vtAC
b) Cho P là 1 điểm thỏa mãn: vtNA + vtNB + vtNC + 6vtPN= vt0. CM P là trung điểm của đoạn NG
c) Tìm x để 3 điểm A, I, M thẳng hàng
Cho tam giác ABC cân đỉnh A.Đỉnh D di động trên AB,E di động,AC sao cho AD=CE.Tìm tập hợp trung điểm I của đoạn DE.
Cho tam giác ABC,M và N di động trên hai cạnh AB,AC sao cho BN=CM.Gọi I là giao điểm của BN và CM. Chứng minh đường phân giác của góc BIC luôn đi qua 1 điểm cố định.
Cảm ơn các bạn nhiều!
Cho tam giác ABC cân tại A; M là 1 điểm di động trên cạnh AB, N là 1 điểm di động trên cạnh AC sao cho AM = CN. Hỏi trung điểm I của MN di động trên đường nào?
Bạn vào link này tham khảo nhé .
https://olm.vn/hoi-dap/question/724228.html
Cho (O) ,đường kính BC , A là điểm di động đường tròn (O) . Gọi I là tâm đường tròn nội tiếp tam giác ABC .Khi A di chuyển trên (O) thì :
A, I thuộc cung chứa góc 135 độ dừng trên đoạn AB .
B, I thuộc cung chứa góc 135 độ dừng trên đoạn AC .
C, I thuộc cung chứa góc 135 độ dừng trên đoạn BC .
D, I thuộc cung chứa góc 45 độ dừng trên đoạn BC .
Cho (O) ,đường kính BC , A là điểm di động đường tròn (O) . Gọi I là tâm đường tròn nội tiếp tam giác ABC .Khi A di chuyển trên (O) thì :
A, I thuộc cung chứa góc 135 độ dừng trên đoạn AB .
B, I thuộc cung chứa góc 135 độ dừng trên đoạn AC .
C, I thuộc cung chứa góc 135 độ dừng trên đoạn BC .
D, I thuộc cung chứa góc 45 độ dừng trên đoạn BC .
Anh em giúp tôi mai mình kiểm tra rồi nhé
C nhé bạn
Công thức của nó có tính góc BIC = 90 + BAC/2=135
Cho tam giác ABC cân tại A .M là trung điểm của BC và I là trung điểm của AC .Chứng minh rằng AM cố định ,B và C di động trên đường thẳng vuông góc với AM sao cho tam giác ABC cân tại A thì sẽ di động trên một đường thẳng cố định
Cho tam giác ABC đều , đường cao AH . M là một điểm di động trên đoạn BH. Kẻ MD , ME lần lượt vuông góc với AB,AC . Gọi I là trung điểm AM. Chứng minh rằng tứ giác IDHE là hình thoi .
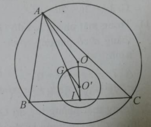
Cho tam giác ABC nội tiếp đường tròn (O). BC cố định, I là trung điểm BC , G là trọng tâm của tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) là ảnh của (O) qua phép vị tự nào sau đây?
A. phép vị tự tâm A tỉ số k = 2/3
B. phép vị tự tâm A tỉ số k = -2/3
C. phép vị tự tâm I tỉ số k = 1/3
D. phép vị tự tâm I tỉ số k = -1/3
B, C cố định nên trung điểm I của BC cũng cố định. G là trọng tâm tam giác ABC nên ta có I G → = 1 / 3 I A → ⇒ có phép vị tự I tỉ số k = 1/3 biến A thành G. A chạy trên (O) nên G chạy trên (O’) ảnh của O qua phép vị tự trên.
Đáp án C
Cho tam giác ABC cân tại A. Gọi D là điểm di động trên cạnh AB. Trên tia đối của tia CB lấy điểm E sao cho BD=CE.CMR:
a,Chu vi tam giác ABC < Chu vi tam giác DAE
b,CMR: Đường thẳng đi qua I vuông góc với DE luôn đi qua 1 điểm cố định khi D di động trên AB