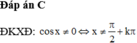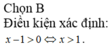điều kiện xác định của hàm số y=sin\(\frac{x-1}{x+1}\)

Những câu hỏi liên quan
Điều kiện xác định của hàm số
y
1
-
sin
x
cos
x
là
Đọc tiếp
Điều kiện xác định của hàm số y = 1 - sin x cos x là
![]()
![]()
![]()
![]()
Tìm tập xác định của hàm số \(y = \frac{1}{{\sin x}}\)
Biểu thức \(\frac{1}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
Đúng 0
Bình luận (0)
Tìm tập xác định của các hàm số sau:
a) \(y = \frac{{1 - \cos x}}{{\sin x}}\);
b) \(y = \sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} .\)
a) Biểu thức \(\frac{{1 - \cos x}}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
b) Biểu thức \(\sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \) có nghĩa khi \(\left\{ {\begin{array}{*{20}{c}}{\frac{{1 + \cos x}}{{2 - \cos x}} \ge 0}\\{2 - \cos x \ne 0}\end{array}} \right.\)
Vì \( - 1 \le \cos x \le 1 ,\forall x \in \mathbb{R}\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\)
Đúng 0
Bình luận (0)
cho hàm số y=f(x)=1/2x-2 tìm điều kiện của x để hàm số y =f(x) xác định
cho hàm số y=f(x)=\(\frac{2x-1}{3x-2}\)
tìm điều kiện của x để hàm số y=f(x) xác định
giải hẳn ra
Điều kiện xác định của hàm số
y
log
2
(
x
-
1
)
là A.
x
≠
1
B. x 1 C. x 1 D.
∀
x
∈
R
Đọc tiếp
Điều kiện xác định của hàm số y = log 2 ( x - 1 ) là
A. x ≠ 1
B. x > 1
C. x < 1
D. ∀ x ∈ R
Điều kiện xác định của hàm số
y
log
2
(
x
-
1
)
là
Đọc tiếp
Điều kiện xác định của hàm số y = log 2 ( x - 1 ) là
![]()
![]()
![]()
![]()
Điều kiện xác định của hàm số
y
log
2
(
x
-
1
)
là
A
.
x
≠
1
B
.
x
1
C
.
x
1
D
.
∀
x...
Đọc tiếp
Điều kiện xác định của hàm số y = log 2 ( x - 1 ) là
A . x ≠ 1
B . x > 1
C . x < 1
D . ∀ x ∈ ℝ
Cho hàm số \(y=f\left(x\right)=\frac{2x-1}{3x-2}\). Tìm điều kiện của x để hàm số\(y=f\left(x\right)\) xác định.
Lời giải:
Để hàm số $f(x)$ xác định thì:
$3x-2\neq 0$
Hay $x\neq \frac{2}{3}$
Đúng 0
Bình luận (0)