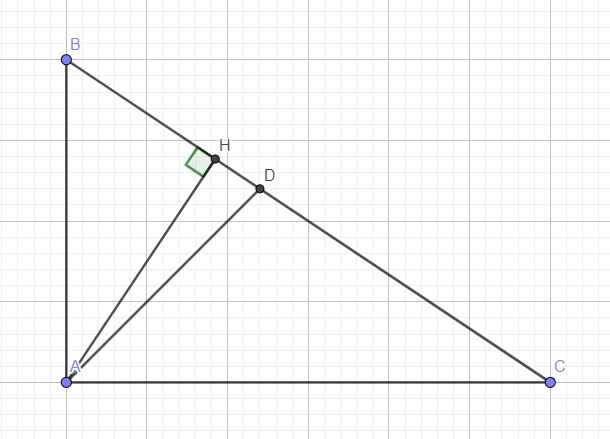
Cho tam giác ABC, đường cao AH, phân giác AD. Biết BH=63cm, CH=112cm. Tính HD

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH, đường phân giác AD. Biết BH=63cm, CH=112cm. Tính HD.
Giúp mình nhé, cảm ơn các bạn nhiều ạ. :))
\(AB^2=HB.BC\)
\(AC^2=HC.BC\)
\(\Rightarrow\frac{HB}{HC}=\frac{AB^2}{AC^2}=\frac{DB^2}{DC^2}=\frac{9}{16}\)
\(\Rightarrow\frac{DB}{DC}=\frac{3}{4}\)
Mà: \(DB=75,DC=100\)
Do H nằm giữa B và D
=> DH = DB- HB = 75 - 64 = 12 (cm)
Đúng 0
Bình luận (1)
Tải app giải toán và kết bạn trao đổi nào cả nhà: https://www.facebook.com/watch/?v=485078328966618
Đúng 0
Bình luận (0)
Tải app giải toán và kết bạn trao đổi nào cả nhà: https://www.facebook.com/watch/?v=485078328966618
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A,đường cao ẠH,đường phân giác AD .Biết BH=63cm,CH=112cm .Tính HD?
Mong các bạn giúp mình!
tam giac ABC vuong tai A, phai ko bạn?
AB^2 = BH . BC
AC^2 = CH. BC
=> BH/CH = AB^2/AC^2 = DB^2/ DC^2 = 9/16 => DB/DC = 3/4 mà DB + DC = BC = 63 + 112 = 175
=> DB = 75, DC = 100
Do H nằm giữa B và D => DH = DB - BH = 12
ủng hộ nha!
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH , phân giác AD biết BH=63cm , CH=112cm
a) tính tỉ số \(\frac{AC}{AB}\)
b) tinh độ dài đoạn thẳng HC
\(\Delta ABC\)vuông tại A đường cao AH, đường phân giác AD. Biết HB=63cm,Hc=112cm
tính bC,AB,AC,HD
Cho ∆ABC vuông ở A, đường cao AH, đường phân giác AD. Biết BH = 63cm, CH = 112 cm.
Tính: a)![]() b)DC c) AD
b)DC c) AD
b: Ta có: BH+CH=BC
nên BC=63+112
hay BC=175cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=63\cdot175\\AC^2=112\cdot175\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=105\left(cm\right)\\AC=140\left(cm\right)\end{matrix}\right.\)
Xét ΔBAC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{105}=\dfrac{CD}{140}\)
mà BD+CD=175
nên Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{BD}{105}=\dfrac{CD}{140}=\dfrac{BD+CD}{105+140}=\dfrac{175}{245}=\dfrac{5}{7}\)
Do đó: CD=100cm
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH, biết AH=4,8cm, BH=3,6cm. a) Tính CH, AB, AC b) Gọi AD là tia phân giác của góc A. Tính BD, CD, HD, AD
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{4.8^2}{3.6}=6.4\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=36\\AC^2=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=6\left(cm\right)\\AC=8\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH , phân giác AD . Biết BD = 7,5cm , CD = 10cm . Tính AH , BH , HD .
Cho tam giác ABC vuông tại A , đường cao AH , phân giác AD . Biết BD = 7,5cm , CD = 10cm . Tính AH , BH , HD .
Ta có: BD+CD=BC(D nằm giữa B và C)
nên BC=7,5+10=17,5(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AB}{AC}=\dfrac{7.5}{10}=\dfrac{3}{4}\)
\(\Leftrightarrow AB=\dfrac{3}{4}AC\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{25}{16}=17.5^2\)
\(\Leftrightarrow AC=14\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{4}\cdot AC=\dfrac{3}{4}\cdot14=10,5\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB\cdot AC=AH\cdot BC\\BH\cdot BC=AB^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH\cdot17.5=10.5\cdot14\\BH\cdot17.5=10.5^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}AH=8,4\left(cm\right)\\BH=6,3\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (2)
Cho tam giác ABC vuông tại A , đường cao AH , phân giác AD . Biết BD = 7,5cm , CD = 10cm . Tính AH , BH , HD .
\(BC=BD+CD=17,5\left(cm\right)\)
Áp dụng định lý phân giác:
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{4}AC\)
Áp dụng Pitago:
\(AB^2+AC^2=BC^2\Leftrightarrow\left(\dfrac{3}{4}AC\right)^2+AC^2=\left(17,5\right)^2\)
\(\Leftrightarrow AC^2=196\Rightarrow AC=14\)
\(\Rightarrow AB=10,5\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=8,4\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=6,3\left(cm\right)\)
\(HD=BD-BH=1,2\left(cm\right)\)
Đúng 1
Bình luận (0)