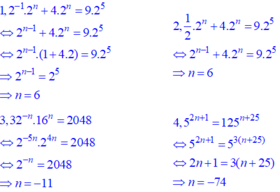A=1/31+1/32+...+1/2048 > 3

Những câu hỏi liên quan
Chứng minh rằng: H = \(\frac{1}{31}+\frac{1}{32}+\frac{1}{33}+....+\frac{1}{2048}\)> 3
Bài siêu dễ cho mấy bạn đây.
A=1/2+1/8+1/32+1/128+1/512+1/2048
Đề bài: Tính
\(A=\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+\frac{1}{128}+\frac{1}{512}+\frac{1}{2048}\)
\(A=\frac{1}{2}+\frac{1}{2^3}+\frac{1}{2^5}+\frac{1}{2^7}+\frac{1}{2^9}+\frac{1}{2^{11}}\)
\(2^2.A=2+\frac{1}{2}+\frac{1}{2^3}+\frac{1}{2^5}+\frac{1}{2^7}+\frac{1}{2^9}\)
\(4A-A=\left(2+\frac{1}{2}+\frac{1}{2^3}+\frac{1}{2^5}+\frac{1}{2^7}+\frac{1}{2^9}\right)-\left(\frac{1}{2}+\frac{1}{2^3}+\frac{1}{2^5}+\frac{1}{2^7}+\frac{1}{2^9}+\frac{1}{2^{11}}\right)\)
\(3A=2-\frac{1}{2^{11}}\)
\(\Rightarrow A=\frac{2-\frac{1}{2^{11}}}{3}\)
Vậy \(A=\frac{2-\frac{1}{2^{11}}}{3}\).
ta có
A= 1/2+ 1/8+1/32+1/128+1/512+1/2048
=> A= 1/2 +1/ 2^3 +1/2^5 +1/2^7+1/2^9+1/2^11
=> 2^2 A=2+1/2+1/2^3+1/2^5+1/2^7+1/2^9
=> 2^2A-A= (2+1/2+1/2^3+1/2^5+1/2^7+1/2^9)-(1/2+1/2^3+/2^5+1/2^7+1/2^9+1/2^11)
=> 3A= 2- 1/2^11
=>3A= 4095/2048
=> A= 1365/2048
A = 1/2-1/4+1/8-1/16+1/32-................-1/1024+1/2048
1/2+1/4+1/8+1/16+1/32+...+1/2048+1/4096
Đặt A=1/2+1/4+1/8+1/16+1/32+...+1/2048+1/4096
\(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{12}}\)
\(2A=2\left(\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{12}}\right)\)
\(2A=1+\frac{1}{2}+...+\frac{1}{2^{11}}\)
\(2A-A=\left(1+\frac{1}{2}+...+\frac{1}{2^{11}}\right)-\left(\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{12}}\right)\)
\(A=1-\frac{1}{2^{12}}\)
Đúng 0
Bình luận (0)
C=3/2+3/4+3/8+3/16+...+3/128
D=1/2+1/4+1/8+...+1/1024
E=5/2+5/8+5/32+5/128+5/512+5/2048
Tìm số nguyên n, biết
1
)
2
−
1
.2
n
+
4.2
n
9.2
5
2
)
1
2
.2
n
+
4.2
n
9.2
5
3...
Đọc tiếp
Tìm số nguyên n, biết
1 ) 2 − 1 .2 n + 4.2 n = 9.2 5
2 ) 1 2 .2 n + 4.2 n = 9.2 5
3 ) 32 − n .16 n = 2048
4 ) 5 2 n + 1 = 125 n + 25
1-1/2-1/4-1/8-1/16-1/32-...-1/1024-1/2048
tính nhanh
Đặt \(A=1-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-..-\frac{1}{2048}\)
\(\Rightarrow A=1-\left(1-\frac{1}{2}\right)-\left(\frac{1}{2}-\frac{1}{4}\right)-..-\left(\frac{1}{1024}-\frac{1}{2048}\right)\)
\(\Rightarrow A=1-1+\frac{1}{2}-\frac{1}{2}+\frac{1}{4}-..-\frac{1}{1024}+\frac{1}{2018}\)
\(\Rightarrow A+\frac{1}{2018}\)
Đúng 1
Bình luận (0)
1-1/2-1/4-1/8-1/16-1/32-1/64-1/128-1/256-1/512-1/1024-1/2048 =0.00048828125
Đúng 0
Bình luận (0)
1+1
2+2
4+4
8+8
16+16
32+32
64+64
128+128
256+256
512+512
1024+1024
2048+2048
1+1=2
2+2=4
4+4=8
8+8=16
16+16=32
32+32=64
64+64=128
128+128 = 256
256+256=512
512+512= 1024
1024+1024 = 2048
2048 + 2048 = 4096
Đúng 0
Bình luận (0)
1+1=2
2+2=4
4+4=8
8+8=16
16+16=32
32+32=64
64+64=128
128+128=256
256+256=512
512+512=1024
1024+1024=2048
2048+2048=4096
Đúng 0
Bình luận (0)
1+1=2
2+2=4
4+4=8
8+8=16
16+16=32
32+32=64
64+64=128
128+128=256
256+256=512
512+512=1024
1024+1024=2048
2048+2048=4096
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1/2+1/4+1/8+1/16+1/32+1/64...+1/2048
Đặt : \(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+......+\frac{1}{2048}\)
\(2A=1+\frac{1}{2}+\frac{1}{4}+.......+\frac{1}{1024}\)
\(2A-A=1-\frac{1}{2048}\)
\(A=\frac{2047}{2048}\)
Good
Đúng 0
Bình luận (0)
S=1/2 +1/4+...+1/2048+1/2048-1/2048
S=1/2+1/4+...+1/1024+1/1024-1/2048
...
S=1-1/2048
S=2047/2048
Đúng 0
Bình luận (0)