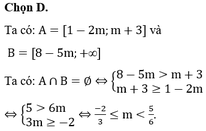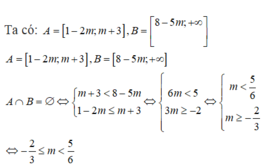1, Cho m là một tham số thực và hai tập hợp A =[ 1-2m; m+3], B = {x thuộc R| x>= 8-5m}. Tìm tất cả các giá trị m để A giao B= rỗng 2, Cho các tập hợp khác rỗng A= ( âm vô cực; m) và B=[ 2m - 2; 2m +2]. Tìm m thuộc R để CR (A hợp B) là một khỏang
Những câu hỏi liên quan
Cho m là một tham số thực và hai tập hợp A[1-2m;m+3],
B
x
∈
R
|
x
≥
8
-
5
m
. Tất cả các giá trị m để
A
∩
B
∅...
Đọc tiếp
Cho m là một tham số thực và hai tập hợp A=[1-2m;m+3], B = x ∈ R | x ≥ 8 - 5 m . Tất cả các giá trị m để A ∩ B = ∅ là:
A. m ≥ 5 6
B. m < - 2 3
C. m ≤ 5 6
D. - 2 3 ≤ m ≤ 5 6
Cho m là một tham số thực và hai tập hợp khác rỗng A [1−2m; m+3], B {
x
∈
R
|
x
≥
8−5m}. Tất cả các giá trị m để
A
∩
B
∅
là: A.
m
≥
5
6
B.
m
5
6
C.
m
≤...
Đọc tiếp
Cho m là một tham số thực và hai tập hợp khác rỗng A = [1−2m; m+3], B = { x ∈ R | x ≥ 8−5m}. Tất cả các giá trị m để A ∩ B = ∅ là:
A. m ≥ 5 6
B. m < 5 6
C. m ≤ 5 6
D. − 2 3 ≤ m < 5 6
$\text{ Cho hai tập hợp M = [ 2m-1;2m+5] và N = [ m+1;m+7] }$
$\text{ ( Với m là tham số thực )}$
$\text{ Hỏi : Tổng }$ tất cả các giá trị của $m$ để hợp của 2 tập hợp $M$ và $N$ là $1$ đoạn có độ dài bằng $10$ là ?
$\text{Help me ! Pls !} $
Đúng 0
Bình luận (0)
cho các tập hợp khác rỗng A=[m-3; 2m] và B=[4-m; 3m-1] với tham số thực m
1, tìm điều kiện của tham số m
2,c/m để AUB là một đoạn
(Em cần lời giải chi tiết ạ! Cảm ơn mọi người)
Câu 1: Tập hợp các giá trị thực của tham số m để phương trình sqrt{x^2+2x+2m}2x+1 có hai nghiệm phân biệt là S (a;b]. Khi đó P a.b là....
Câu 2: Cho phương trình sqrt{-x^2+4x-3}sqrt{2m+3x-x^2}. Để phương trình có nghiệm thì m ϵ [a;b]. Giá trị a^2+b^2?
Câu 3: Biết phương trình x^4-3mx^2+m^2+10 có 4 nghiệm phân biệt x_1,x_2,x_3,x_4. Tính M x1+x2+x3+x4+x1x2x3x4
Đọc tiếp
(Em cần lời giải chi tiết ạ! Cảm ơn mọi người)
Câu 1: Tập hợp các giá trị thực của tham số m để phương trình \(\sqrt{x^2+2x+2m}=2x+1\) có hai nghiệm phân biệt là S = (a;b]. Khi đó P = a.b là....
Câu 2: Cho phương trình \(\sqrt{-x^2+4x-3}=\sqrt{2m+3x-x^2}\). Để phương trình có nghiệm thì m ϵ [a;b]. Giá trị \(a^2+b^2=?\)
Câu 3: Biết phương trình \(x^4-3mx^2+m^2+1=0\) có 4 nghiệm phân biệt \(x_1,x_2,x_3,x_4\). Tính M = x1+x2+x3+x4+x1x2x3x4
1.
\(2x+1\ge0\Rightarrow x\ge-\dfrac{1}{2}\)
Khi đó pt đã cho tương đương:
\(x^2+2x+2m=\left(2x+1\right)^2\)
\(\Leftrightarrow x^2+2x+2m=4x^2+4x+1\)
\(\Leftrightarrow3x^2+2x+1=2m\)
Xét hàm \(f\left(x\right)=3x^2+2x+1\) trên \([-\dfrac{1}{2};+\infty)\)
\(-\dfrac{b}{2a}=-\dfrac{1}{3}< -\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{2}\right)=\dfrac{3}{4}\) ; \(f\left(\dfrac{1}{3}\right)=\dfrac{2}{3}\)
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb khi và chỉ khi \(\dfrac{2}{3}< 2m\le\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{1}{3}< m\le\dfrac{3}{8}\)
\(\Rightarrow P=\dfrac{1}{8}\)
Đúng 1
Bình luận (0)
3.
Đặt \(x^2=t\ge0\Rightarrow\left[{}\begin{matrix}x=\sqrt{t}\\x=-\sqrt{t}\end{matrix}\right.\)
Pt trở thành: \(t^2-3mt+m^2+1=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=9m^2-4\left(m^2+1\right)>0\\t_1+t_2=3m>0\\t_1t_2=m^2+1>0\end{matrix}\right.\) \(\Rightarrow m>\dfrac{2}{\sqrt{5}}\)
Ta có:
\(M=x_1+x_2+x_3+x_4+x_1x_2x_3x_4\)
\(=-\sqrt{t_1}-\sqrt{t_2}+\sqrt{t_1}+\sqrt{t_2}+\left(-\sqrt{t_1}\right)\left(-\sqrt{t_2}\right)\sqrt{t_1}.\sqrt{t_2}\)
\(=t_1t_2=m^2+1\) với \(m>\dfrac{2}{\sqrt{5}}\)
Đúng 1
Bình luận (0)
2.
ĐKXĐ: \(1\le x\le3\)
Pt tương đương:
\(-x^2+4x-3=2m+3x-x^2\)
\(\Leftrightarrow x=2m+3\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(1\le2m+3\le3\)
\(\Leftrightarrow-1\le m\le0\)
\(\Rightarrow a^2+b^2=1\)
Đúng 1
Bình luận (0)
cho các tập hợp khác rỗng A=[m-3; 2m] và B=[4-m; 3m-1] với tham số thực m
1, tìm điều kiện của tham số m
2,c/m để AUB là một đoạn
1) vì các tập hợp \(A;B\) khác tập rỗng \(\Rightarrow\left\{{}\begin{matrix}m-3\le2m\\4-m\le3m-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge-3\\m\ge\dfrac{5}{4}\end{matrix}\right.\) \(\Rightarrow m\ge\dfrac{5}{4}\) vậy \(m\ge\dfrac{5}{4}\)
2) vì \(m\ge\dfrac{5}{4}\) \(\Rightarrow m-3< 3m-1\)
\(\Rightarrow A\cup B=\left[m-3;2m\right]\cup\left[4-m;3m-1\right]=\left[m-3;3m-1\right]\)
\(\Rightarrow\) (đpcm)
Đúng 0
Bình luận (0)
Cho hai tập hợp A=(m+1;m+5) B=[2m-1;2m+6]. Tìm các giá trị của tham số m sao cho A ∩ B ≠ ∅
Cho hai tập hợp A [m; m+1] và B [0;3). Tìm tất cả các giá trị thực của tham số m để A
∩
B
∅
A.
m
∈
(
−
∞
;
−
1
)
∪
(
3
;
+
∞
)
.
B.
m
∈
(
−
∞
;
−
1...
Đọc tiếp
Cho hai tập hợp A = [m; m+1] và B = [0;3). Tìm tất cả các giá trị thực của tham số m để A ∩ B = ∅
A. m ∈ ( − ∞ ; − 1 ) ∪ ( 3 ; + ∞ ) .
B. m ∈ ( − ∞ ; − 1 ] ∪ ( 3 ; + ∞ ) .
C. m ∈ ( − ∞ ; − 1 ) ∪ [ 3 ; + ∞ ) .
D. m ∈ ( − ∞ ; − 1 ] ∪ [ 3 ; + ∞ ) .
Tập hợp tất cả các giá trị thực của tham số m để hàm số
y
m
+
1
x
+
2
m
+
2
x
+
m
nghịch biến trên khoảng
-
1
;...
Đọc tiếp
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = m + 1 x + 2 m + 2 x + m nghịch biến trên khoảng - 1 ; + ∞ là
A. - 1 ; 2
B. 2 ; + ∞
C. - ∞ ; 1 ∪ 2 ; + ∞
D. [ 1;2)
