Cho tam giác ABC cân A ,H là trung điểm BC, I là trung điểm AC, E đối xứng H qua I. Tứ giác AHCE là hình gì?Chứng minh.

Những câu hỏi liên quan
Bài 5 : (2.5 điểm )
Cho tam giác ABC cân tại A.Kẻ AH vuông góc với BC ( H thuộc BC ).Gọi I là trung điểm của AC,E là điểm đối xứng với H qua Y
A ) Chứng minh tứ giác AHCE là hình chữ nhật
B ) Chứng minh tứ giác AHCE là hình bình hành
Xét △AIE Và △CIH có
IA=IC(gt)
IH=IE(gt)
^AIE=^CIH(đối đỉnh)
⇒△AIE =△CIH(c-g-c)
⇒AE=HC(2 cạnh tương ứng)
⇒^IAE=^ICH(2 góc tương ứng)
mà 2 góc này có vị trí so le trong
⇒AE // HC
Xét tứ giác AHCE có AE // HC (cmt)
AE=HC
⇒AHCE là hình bình hành có ^AHC=900
⇒AHCE là hình chữ nhật
Đúng 1
Bình luận (0)
Bài 5 : (2.5 điểm )
Cho tam giác ABC cân tại A.Kẻ AH vuông góc với BC ( H thuộc BC ).Gọi I là trung điểm của AC,E là điểm đối xứng với H qua Y
A ) Chứng minh tứ giác AHCE là hình chữ nhật
B ) Chứng minh tứ giác AHCE là hình bình hành
Câu cuối rồi giúp với ạ
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Chứng minh tứ giác AHCE là hình chữ nhật.
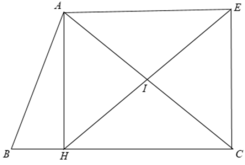
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có E A H ^ = A H C ^ = H C E ^ = C E A ^ = 90 0
⇒ AHCE là hình chữ nhật.
Đúng 0
Bình luận (0)
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I.
a) Tứ giác AHCE là hình gì? Chứng minh
b) Gọi K, M, N là trung điểm AB, HB, HC. Chứng minh KN = IM
a: Xét tứ giác AHCE có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
b: Xét ΔAHB có
K là trung điểm của AB
M là trung điểm của BH
Do đó: KM là đường trung bình của ΔAHB
Suy ra: KM//AH
hay KM\(\perp\)BH
Xét ΔAHC có
I là trung điểm của AC
N là trung điểm của HC
Do đó: IN là đường trung bình của ΔAHC
Suy ra: IN//AH
hay IN\(\perp\)BC
Xét ΔABC có
K là trung điểm của AB
I là trung điểm của AC
Do đó: KI là đường trung bình của ΔBAC
Suy ra: KI//BC
hay KI\(\perp\)AH
mà AH//KM
nên KI\(\perp\)KM
Xét tứ giác KINM có
\(\widehat{IKM}=\widehat{KMN}=\widehat{INM}=90^0\)
Do đó: KINM là hình chữ nhật
Suy ra: KN=IM
Đúng 0
Bình luận (0)
cho tam giác abc có góc a = 90° . M là trung điểm BC . D , E lần lượt là trung điểm của AB , AC . a) chứng minh tứ giác ADHE là hcn b) lấy I đối xứng D qua H . Tứ giác ADIC là hình gì ? c) lấy K đối xứng E qua H . Tứ giác AEKB là hình gì ? d) chứng minh DK // EI
a: Xét ΔCBA có
H là trung điểm của BC
E là trung điểm của AC
Do đó: HE là đường trung bình của ΔCBA
Suy ra: HE//AB và \(HE=\dfrac{AB}{2}\)
hay HE//AD và HE=AD
Xét tứ giác ADHE có
HE//AD
HE=AD
Do đó: ADHE là hình bình hành
mà \(\widehat{EAD}=90^0\)
nên ADHE là hcn
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC), đường cao AH, gọi D là trung điểm của AC, lấy điểm E đối xứng với H qua D.a) Chứng minh tứ giác AHCE là hình chữ nhậtb) Qua A kẻ AI song song với HE (I ∈ đường thẳng BC). Chứng minh tứ giác AEHI là hình bình hành.c) Trên tia đối của tia HA lấy điểm K sao cho AH HK. Chứng minh AK là tia phân giác của góc IAC.d) Tìm điều kiện của tam giác ABC để tứ giác CAIK là hình vuông, khi đó tứ giác AHCE là hình gì?
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH, gọi D là trung điểm của AC, lấy điểm E đối xứng với H qua D.
a) Chứng minh tứ giác AHCE là hình chữ nhật
b) Qua A kẻ AI song song với HE (I ∈ đường thẳng BC). Chứng minh tứ giác AEHI là hình bình hành.
c) Trên tia đối của tia HA lấy điểm K sao cho AH = HK. Chứng minh AK là tia phân giác của góc IAC.
d) Tìm điều kiện của tam giác ABC để tứ giác CAIK là hình vuông, khi đó tứ giác AHCE là hình gì?
a: Xét tứ giác AHCE có
D là trung điểm của AC
D là trung điểm của HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC), đường cao AH, gọi D là trung điểm của AC, lấy điểm E đối xứng với H qua D.a) Chứng minh tứ giác AHCE là hình chữ nhậtb) Qua A kẻ AI song song với HE (I ∈ đường thẳng BC). Chứng minh tứ giác AEHI là hình bình hành.c) Trên tia đối của tia HA lấy điểm K sao cho AH HK. Chứng minh AK là tia phân giác của góc IAC.d) Tìm điều kiện của tam giác ABC để tứ giác CAIK là hình vuông, khi đó tứ giác AHCE là hình gì?
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH, gọi D là trung điểm của AC, lấy điểm E đối xứng với H qua D.
a) Chứng minh tứ giác AHCE là hình chữ nhật
b) Qua A kẻ AI song song với HE (I ∈ đường thẳng BC). Chứng minh tứ giác AEHI là hình bình hành.
c) Trên tia đối của tia HA lấy điểm K sao cho AH = HK. Chứng minh AK là tia phân giác của góc IAC.
d) Tìm điều kiện của tam giác ABC để tứ giác CAIK là hình vuông, khi đó tứ giác AHCE là hình gì?
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì? Vì sao?
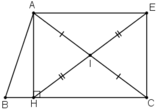
I là trung điểm của AC ⇒ IA = IC.
E đối xứng với H qua I ⇒ IE = IH
⇒ AC ∩ HE = I là trung điểm của AC và HE
⇒ AHCE là hình bình hành (dấu hiệu nhận biết 4)
Lại có : Ĥ = 90º
⇒ AHCE là hình chữ nhật (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là trung điểm AC. Lấy điểm E đối xứng với điểm H qua D.a) Chứng minh tứ giác AHCE là hình chữ nhậtb) Kẻ AI // HE(I thuộc BC). Chứng minh tứ giác AIHE là hình bình hànhc) Trên tia đối của tia HA lấy điểm K sao cho AH HK. Chứng minh tứ giác AIKC là hình thoid) Tam giác ABC có thêm điều kiện gì để CAIK là hình vuông? Khi đó tứ giác AHCE là hình gì?
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là trung điểm AC. Lấy điểm E đối xứng với điểm H qua D.
a) Chứng minh tứ giác AHCE là hình chữ nhật
b) Kẻ AI // HE(I thuộc BC). Chứng minh tứ giác AIHE là hình bình hành
c) Trên tia đối của tia HA lấy điểm K sao cho AH = HK. Chứng minh tứ giác AIKC là hình thoi
d) Tam giác ABC có thêm điều kiện gì để CAIK là hình vuông? Khi đó tứ giác AHCE là hình gì?
a ) Xét ◇AHCE có :
D là trung điểm HE
D là trung điểm AC
\(\Rightarrow\)◇AHCE là hình bình hành
Mà góc AHC = 90°
\(\Rightarrow\)◇AHCE là hình chữ nhật
b ) Xét ◇AEIH có :
AI // HE ( giả thiết )
AE // IH ( do I \(\in\)BC và AE // BC )
\(\Rightarrow\)◇AEIH là hình bình hành























