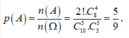Áp dụng AM-GM có:

\(2a^2+2b^2\ge4ab\)

\(8b^2+\dfrac{1}{2}c^2\ge4bc\)

\(8a^2+\dfrac{1}{2}c^2\ge4ac\)

Cộng vế với vế \(\Rightarrow VT\ge4\left(ab+bc+ac\right)=4\)

Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}ab+bc+ac=1\\a=b=\dfrac{c}{4}\end{matrix}\right.\)\(\Rightarrow a=b=\dfrac{1}{3};c=\dfrac{4}{3}\)

Đáp án C

Phương pháp: Thêm bớt hạng tử để được các hằng đẳng thức.

Sử dụng kết quả A 2 + B 2 + C ≥ C  để tìm min F và chú ý tìm điều kiện để dấu “=” xảy ra. 2

Cách giải:  F = a 4 b 4 + b 4 a 4 − a 2 b 2 + b 2 a 2 + a b + b a

= a 2 b 2 − 1 2 + b 2 a 2 − 1 2 + a b + b a 2 + a b + b a − 4 ≥ a 2 + b 2 a b − 4 ≥ 2 − 4 = − 2

Dấu “=” xảy ra ⇔ a ; b = − 1 ; 1  hoặc  a ; b = 1 ; − 1

Vậy M i n y = − 2  tại a ; b = − 1 ; 1  hoặc a ; b = 1 ; − 1

Câu 3: 

#include <bits/stdc++.h>

using namespace std;

long long n;

int main()

{

cin>>n;

bool kt=true;

for (long long i=2; i<=sqrt(n); i++)

if (n%i==0) 

{

kt=false;

break;

}

if ((kt==true) and (n>1)) cout<<"la so nguyen to";

else cout<<"khong la so nguyen to";

return 0;

}

Giúp mình với ạ

Giúp mình với

Chọn A

+ Chia đều 10 đội vào 2 bảng A và B có  cách.

Do đó số phần tử của không gian mẫu là : 

+ Sắp xếp  đội của  lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.

Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4  cách.

Bốn đội còn lại xếp vào bảng còn lại.

Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là 

Gọi A là biến cố  “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ”  thì số các kết quả thuận lợi  cho biến cố A là:

+ Xác suất cần tìm là: 

Đáp án A

Phương pháp: Sử dụng phương pháp tích phân từng phần tính F(x)

Cách giải:

=>