Tìm các số a và b thỏa mãn một trong các điều kiện sau : a+b=|b|-|a|

Những câu hỏi liên quan
Tìm các số a và b thỏa mãn một trong các điều kiện sau:
a) a + b = /a/ + /b/
b)a + b = /b/ - /a/
\(a+b=\left|a\right|+\left|b\right|\)
Ta có: \(\hept{\begin{cases}\left|a\right|\ge a\forall x\\\left|b\right|\ge b\forall b\end{cases}\Rightarrow}\left|a\right|+\left|b\right|\ge a+b\forall a;b\)
Mà \(a+b=\left|a\right|+\left|b\right|\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\left|a\right|=a\\\left|b\right|=b\end{cases}}\Leftrightarrow\hept{\begin{cases}a\ge0\\b\ge0\end{cases}}\)
Vậy \(a\ge0;b\ge0\)
Đúng 0
Bình luận (0)
1) Tìm các số a,b thỏa mãn trong các điều kiện sau:
a + b = | b | - | a |
2) Có bao nhiêu cặp số nguyên (x,y) thỏa mãn một trong các điều kiện sau:
| x | + | y | = 20
| x | + | y | < 20
(Các cặp số (3 ; 4) và (4 ; 3) là hai cặp số khác nhau).
Tìm các số a và b thỏa mãn 1 trong các điều kiện sau :
a ) a + b = | a | + | b |
b ) a + b = | b | - | a |
a, Xét 2 trường hợp có thể xảy ra
TH1:Nếu b> hoặc =0 thì a+b=|a|+b, khi đó a=|a| hay a> hoặc =0
TH2: Nếu b<0 thì a+b=|a|-b, khi đó |a|-a=2b.Đẳng thức này ko xảy ra vì vế trái ko âm,vế phải âm
Vậy a> hoặc =0,b> hoặc =0 là các giá trị thỏa mãn a+b=|a|+|b|
Đúng 0
Bình luận (0)
1 Tìm giá trị nhỏ nhất của bểu thức Cfrac{6}{left|xright|-3} với x là số nguyên2 . Tìm giá trị lớn nhất của biểu thức x-|x|3 . Tìm các số a và b thỏa mãn một điều trong các điều kiện sau :a ) a+b |a| + |b|b ) a+b |b| - |a|4 . Có bao nhiêu cặp số nguyên (x;y) thỏa mãn một trong các điều kiện sau :a ) |x| + |y| 20b) |x| + |y| 20( Các cặp số (3;4) và (4;3) là 2 cặp số khác nhau )
Đọc tiếp
1 Tìm giá trị nhỏ nhất của bểu thức \(C=\frac{6}{\left|x\right|-3}\) với x là số nguyên
2 . Tìm giá trị lớn nhất của biểu thức x-|x|
3 . Tìm các số a và b thỏa mãn một điều trong các điều kiện sau :
a ) a+b = |a| + |b|
b ) a+b = |b| - |a|
4 . Có bao nhiêu cặp số nguyên (x;y) thỏa mãn một trong các điều kiện sau :
a ) |x| + |y| = 20
b) |x| + |y| <20
( Các cặp số (3;4) và (4;3) là 2 cặp số khác nhau )
1)
Xét \(\left|x\right|>3\)\(\Rightarrow\)\(C>0\)
Xét \(0\le\left|x\right|< 3\)\(\Rightarrow\)\(C< 0\)
+ Với \(\left|x\right|=0\)\(\Leftrightarrow\)\(x=0\) thì \(C=-2\)
+ Với \(\left|x\right|=1\)\(\Leftrightarrow\)\(x=\pm1\) thì \(C=-3\)
+ Với \(\left|x\right|=2\)\(\Leftrightarrow\)\(x=\pm2\) thì \(C=-6\)
Vậy GTNN của \(C=-6\) khi \(x=\pm2\)
2)
Xét \(x\ge0\)\(\Rightarrow\)\(x-\left|x\right|=0\)
Xét \(x< 0\)\(\Rightarrow\)\(x-\left|x\right|=2x< 0\)
Vậy GTLN của \(x-\left|x\right|=0\) khi \(x>0\)
Ví dụ một bài toán :
Tìm GTLN của B = 10-4 | x-2|
Vì |x-2| \(\ge0\forall x\)
\(\Rightarrow-4.\left|x-2\right|\le0\forall x\). Tại sao mà tìm GTLN mà lại nhỏ hơn hoặc bằng 0 ạ
Còn một bài : Tìm GTNN của biểu thức A=2|3x-1| -4
Vì |3x-1| \(\ge0\)
\(\Rightarrow2\left|3x-1\right|\ge0\forall x\) cái này là timg GTNN mà giờ lại lớn hơ hoặc bằng 0 ạ
Xem thêm câu trả lời
tìm cac số nguyên (x;y) thỏa mãn một trong các điều kiện sau :a+b=|b|-|a|
giải giúp mk vs
Tìm phân số a/b thỏa mãn các điều kiện sau 4/9<a/b<10/21 và 5a-2b=3
Tìm các số a và b thỏa mãn các điều kiện sau :
a ) a + b = | a | + | b |
b ) a + b = | b | - | a |
Vì |a| và |b| >= 0 nên để a+b=|a|+|b| thì a và b >= 0
Vậy để a+b=|a|+|b| thì a;b€N
Đúng 0
Bình luận (0)
Cho hàm số y = ax + b .Tìm a và b, biết rằng đồ thị của hàm số đã cho thỏa mãn một trong các điều kiện sau:
a) Đi qua hai điểm A(1; 3) và B(-1; -1).
b) Song song với đường thẳng y = x + 5 và đi qua điểm C(1; 2).
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
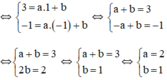
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
Đúng 0
Bình luận (0)
Cho hàm số y = ax + b .Tìm a và b, biết rằng đồ thị của hàm số đã cho thỏa mãn một trong các điều kiện sau:
a) Đi qua hai điểm A(1; 3) và B(-1; -1).
b) Song song với đường thẳng y = x + 5 và đi qua điểm C(1; 2).
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
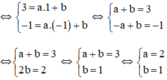
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
Đúng 0
Bình luận (0)
Tìm tất cả các bộ số nguyên dương ( a, b, c, d) thỏa mãn đồng thời các điều kiện sau:
ab=c+d và a+b=cd















