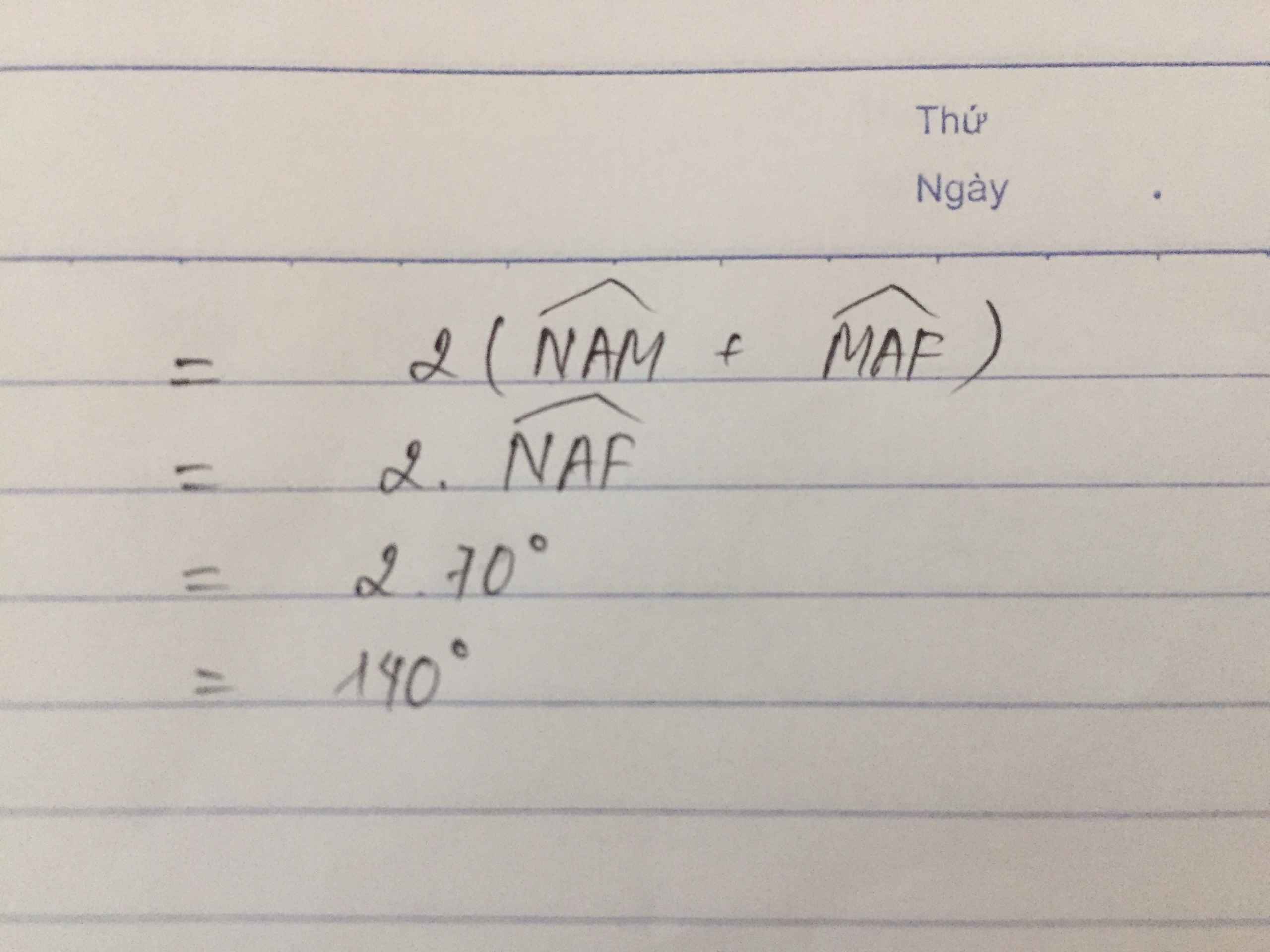Cho tam giác đều ABC cạnh 5cm. Qua A kẻ d // BC. Vẽ D đối xứng của C qua d. Tính CD.

Những câu hỏi liên quan
Cho tam giác đều ABC cạnh 5cm. Qua A kẻ d // BC. Vẽ D đối xứng của C qua d. Tính CD. (Mấy bạn vẽ hình nha.)
Cho tam giác ABC đều , cạnh dài 2 cm , đường cao AH .
a) Vẽ D đối xứng vs A qua BC
b) Cm tứ giác ABCD là hình thoi
c) Tính diện tích tam giác ABC
d) Lấy điểm M trên cạnh BD ( M ko trùng B và D ) . Cm ddierm đối xứng của M qua H nằm giữa A và C .
cho tam giác ABC đường cao AH. các đường trung tuyến BM, CN. gọi D là điểm đối xứng của B qua M. E là điểm đối xứng C qua N. a) tứ giác ABC là hình gì? b) Chứng minh D, E đối xứng qua A c) cho tam giác ABC có AB=AC=5cm, BC=8cm. Tính diện tích ABCD
a: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
b: Xét tứ giác AEBC có
N là trung điểm chung của AB và EC
nên AEBC là hình bình hành
=>AE//BC và AE=BC
=>AD//AE và AD=AE
=>A là trung điểm của DE
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, AB 5cm, BC 13 cm. Gọi D là trung điểm của AC. Vẽ điểm E đối xứng với điểm B qua D.a) Tính độ dài cạnh AC.b) Chứng minh tứ giác ABCE là hình bình hành. c) Gọi M là điểm đối xứng với B qua A. Tứ giác AMEC là hình gì ? Vì sao?
Đọc tiếp
Cho tam giác ABC vuông tại A, AB = 5cm, BC = 13 cm. Gọi D là trung điểm của AC. Vẽ điểm E đối xứng với điểm B qua D.
a) Tính độ dài cạnh AC.
b) Chứng minh tứ giác ABCE là hình bình hành.
c) Gọi M là điểm đối xứng với B qua A. Tứ giác AMEC là hình gì ? Vì sao?
Hình Tự Vẽ Nhe
a)
Áp dụng định lí PItago vào tam giác ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2=13^2-5^2=12\left(cm\right)\)
b)
Tứ Giác ABCE có:
D là trung điểm của AC (gt)
D là trung điểm của BE ( E đối xứng B qua A )
=> Tứ Giác ABCE là Hình Bình Hành
c)
Ta có:
Vì tứ giác ABCE là hình bình hành => CE=AB; CE//AB ( tính chất hình bình hành ) (1)
Mà M đối xứng với B qua A => AM=AB (2)
CE//AB (cmt) => CE//AM (3)
Từ (1) và (2) (3) => CE//AM và CE=AM
Tứ Giác AMEC có:
CE=AM (cmt)
CE//AM (cmt)
Góc A = 90 độ (gt)
=> Tứ giác AMEC là Hình Chữ Nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC kẻ các phân giác BE,CF, gọi D là điểm đối xứng của điểm E qua đường thẳng CF
a, Chứng minh rằng điểm D nằm trên cạnh BC
b, Xét trường hợp điểm D cũng cũng là điểm đối xứng của điểm F qua đường thẳng BE .Chứng minh rằng tam giác DEF là tam giác đều .Và tính góc A
Cho tam giác ABC vuông tại B, D là trung điểm của AC. Qua D kẻ DE//BC(E thuộc AB) và DF//AB (F thuộc BC).
a) Chứng minh tứ giác BEDF là hình chữ nhật
b) Vẽ M đối xứng với D qua E, N đối xứng với D qua F. Chứng minh M,B,N thẳng hàng
c) Tính diện tích tam giác DEF biết diện tích tam giác ABC là 24cm vuông.
a, Ta có: DE//BC \(\Rightarrow\widehat{DEB}+\widehat{EBF}=180\)
mà góc EBF =90 => góc DEB =90 (1)
Chứng minh tương tự với DF//AB
\(\Rightarrow\widehat{EDF}=90;\widehat{BFD}=90\) (2)
Từ (1) và (2) => tứ giác BEDF là hình chữ nhật
Đúng 0
Bình luận (0)
a) vì ED//BC và DF//AB
Mà \(\Delta ABC\)vuông tại B
Nên \(DE\perp AB\)và \(DF\perp BC\)
Xét tứ giác BEDF có:
\(\widehat{B}=\widehat{DEB}=\widehat{DFB}=90^0\)
Vậy tứ giác BEDF là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC đều có đường cao AH. Trên cạnh BC lấy điểm D bất kì. Gọi E là điểm đối xứng D qua AB, F là điểm đối xứng của D qua AC. Kẻ EM vuông góc với BC, FN vuông góc với BC. Cm EM+FN=AH
BÀI 1: Cho tam giác ABC. Trên tia đối của tia BA lấy D, trên tia đối của tia CA lấy E sao cho BD = CE = BC. Gọi M là giao điểm của BE và CD đường thẳng qua M song song với tia phân giác của góc BAC cắt AC ở F. Chứng minh rằng AB = CF.
BÀI 2:Cho tam giác đều ABC, điểm M thuộc cạnh BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đối xứng với M qua AC. Vẽ hình bình hành MDNE. CMR: AN // BC.
“““““` ✬ ‘✧ ‘✬
““““` __♜_♜_♜__
“““` `{,,,,,,,,,,,,,,,,,,,,,}
‘“` ✩`{✫//✰//✰//✫}` ✩
‘“` ♖_{♖___♖__♖___.♖}_♖
“` {///////////////}
“`{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}
“{//////////////////}
“{_✿__❀_♥_✿_♥_❀__✿_}
““““ * ` ` * ` ` *
‘““““ 0 ` ` 0 ` ` 0
““““ ||___||___||
““ * ` {,,,,,,,,,,,,,,,,,,,} ` *
““ 0 ` {////////} ` 0
‘“`_||_{_______”_____}_||_
“`{///////////////}
“`{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}
“`{///////////////}
“`{_____________”________}
Đúng 0
Bình luận (0)
cho abc tia phan giac cua goc b cat ac o d tren tia doi cua tia ba lay e sao cho be = bc chung minh bd song song ec cai nay lam sao
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A =70 độ, điểm M thuộc cạnh BC vẽ D đối xứng M qua AB, E đối xứng M qua AC
a, CM AD=AE
b, Tính DAE
VẼ HÌNH