với giá trị nào của m thì phương trình (m+10 sinx + cosx=\(\sqrt{5}\) có nghiệm

Những câu hỏi liên quan
1, cho phương trình sin2x-left(2m+sqrt{2}right)left(sinx+cosxright)+2msqrt{2}+10 tìm các giá trị m để phương trình có đúng 2 nghiệm xinleft(0;dfrac{5Pi}{4}right)2,tìm tất cả các giá trị thực của tham số m để phương trình cos2x+left(2m+1right)sinx-m-10 có đúng 2 nghiệm thuộc khoảng left(dfrac{Pi}{2};dfrac{3Pi}{2}right)3, cho phương trình cos^2x-2mcosx+6m-90 tìm các giá trị m để phương trình có nghiệm thuộc khoảng left(-dfrac{Pi}{2};dfrac{Pi}{2}right)
Đọc tiếp
1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)
2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)
3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm thuộc khoảng \(\left(-\dfrac{\Pi}{2};\dfrac{\Pi}{2}\right)\)
Tìm giá trị của tham số m để phương trình
sin
x
−
1
cos
2
x
−
cos
x
+
m
0
có đúng 5 nghiệm thuộc đoạn
0
;
2
π
A. ...
Đọc tiếp
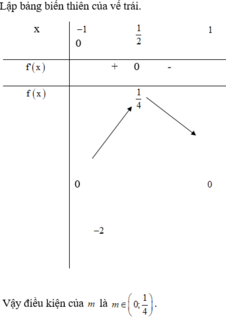
Tìm giá trị của tham số m để phương trình sin x − 1 cos 2 x − cos x + m = 0 có đúng 5 nghiệm thuộc đoạn 0 ; 2 π
A. 0 ≤ m < 1 4
B. − 1 4 < m ≤ 0
C. 0 < m < 1 4
D. − 1 4 < m < 0
Đáp án C
Phương trình
sin x − 1 cos 2 x − cos x + m = 0 ⇔ sin x = 1 m = cos x − cos 2 x ⇔ x = π 2 + k 2 π 1 m = cos x − cos 2 x 2
Vì x ∈ 0 ; 2 π nên
0 ≤ π 2 + k 2 π ≤ 2 π ⇔ − 1 4 ≤ k ≤ 3 4 ⇒ k = 0 ⇒ x = π 2
Để phương trình đã cho có 5 nghiệm thuộc đoạn 0 ; 2 π ⇔ 2 có 4 nghiệm phân biệt thuộc 0 ; 2 π
Đặt t = cos x ∈ − 1 ; 1 , khi đó 2 ⇔ t 2 − t + m = 0 có 2 nghiệm phân biệt t 1 , t 2 thỏa mãn − 1 < t 1 ; t 2 < 1
⇔ t 1 + 1 t 2 + 1 > 0 t 1 − 1 t 2 − 1 > 0 Δ = − 1 2 − 4 m > 0 ⇔ t 1 t 2 + t 1 + t 2 + 1 > 0 t 1 t 2 − t 1 + t 2 + 1 > 0 − 4 m − 1 < 0 ⇔ 0 < m < 1 4
Vậy m ∈ 0 ; 1 4
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để phương trình :
s
inx
2019
−
c
os
2
x
2018
−
cos
x
+
m
2019
−
sin
2
x...
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình :
s inx 2019 − c os 2 x 2018 − cos x + m 2019 − sin 2 x + m 2 + 2 m cos x 2018 = cos x − s inx + m có nghiệm thực
A. 1
B. 3
C. 2
D. 0
Đáp án B
Phương pháp:
Sử dụng phương pháp hàm số để giải phương trình.
Cách giải :
s inx 2019 − cos 2 x 2018 − cos x + m 2019 − sin 2 x + m 2 + 2 m cos x 2018 = cos x − s inx + m
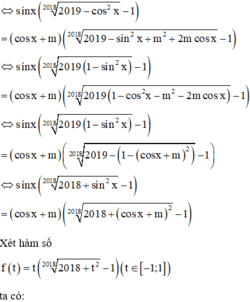
f ' t = 2018 + t 2 2018 − 1 + t . 1 2018 2018 + t 2 − 2017 2018 .2 t ≥ 0 ∀ t ∈ − 1 ; 1 Suy ra

Đúng 0
Bình luận (0)
Tìm các giá trị thực của tham số m để phương trình
(
sin
x
-
1
)
.
(
cos
2
x
-
cos
x
+
m
)
0
có đúng 5 nghiệm thuộc đoạn
0
,...
Đọc tiếp
Tìm các giá trị thực của tham số m để phương trình ( sin x - 1 ) . ( cos 2 x - cos x + m ) = 0 có đúng 5 nghiệm thuộc đoạn 0 , 2 π
A . 0 ≤ m ≤ 1 4
B . - 1 4 ≤ m ≤ 0
C . 0 ≤ m ≤ 1 4
D . - 1 4 < m < 0
Cho phương trình
sin
2
x
+
2
m
-
1
sin
x
cos
x
-
m
+
1
cos
2
x
m
Với giá trị nào của m thì phương trình đã cho có nghiệ...
Đọc tiếp
Cho phương trình
sin 2 x + 2 m - 1 sin x cos x - m + 1 cos 2 x = m
Với giá trị nào của m thì phương trình đã cho có nghiệm?
A. m ≥ 1
B. - 3 < m < 0
C. m ≤ 1
D. - 2 ≤ m ≤ - 1
Có bao nhiêu giá trị nguyên của tham số m để phương trình
sin
x
cos
x
−
sin
x
−
cos
x
+
m
0
có nghiệm? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin x cos x − sin x − cos x + m = 0 có nghiệm?
A. 1
B. 2
C. 3
D. 4
Đặt t = sin x + cos x − 2 ≤ t ≤ 2 ⇒ sin x cos x = t 2 − 1 2 .
Phương trình trở thành t 2 − 1 2 − t + m = 0 ⇔ − 2 m = t 2 − 2 t − 1 ⇔ t − 1 2 = − 2 m + 2 .
Do − 2 ≤ t ≤ 2 ⇒ − 2 − 1 ≤ t − 1 ≤ 2 − 1 ⇔ 0 ≤ t − 1 2 ≤ 3 + 2 2 .
Vậy để phương trình có nghiệm
⇔ 0 ≤ − 2 m + 2 ≤ 3 + 2 2 ⇔ − 1 + 2 2 2 ≤ m ≤ 1 → m ∈ ℤ m ∈ − 1 ; 0 ; 1 .
Chọn đáp án C.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để phương trình
3
sinx-cosx m có nghiệm trên đoạn
π
6
;
7
π
6
? A. 2. B. 3. C. 4 D. 5.
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình 3 sinx-cosx = m có nghiệm trên đoạn π 6 ; 7 π 6 ?
A. 2.
B. 3.
C. 4
D. 5.
Tìm tất cả giá trị của m để phương trình sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m có nghiệm?
A. 0 ≤ m ≤ 1
B.m> 1
C.0< m< 1
D. m ≤ 0
Hướng dẫn giải:
Chọn A.
Ta có: sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m
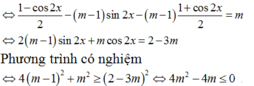
![]()
Đúng 0
Bình luận (0)
Số giá trị nguyên của tham số m để phương trình
sin
x
+
(
m
−
1
)
cos
x
2
m
−
1
có nghiệm là A. 0 B. 3 C. 2 D. 1
Đọc tiếp
Số giá trị nguyên của tham số m để phương trình sin x + ( m − 1 ) cos x = 2 m − 1 có nghiệm là
A. 0
B. 3
C. 2
D. 1
Số giá trị nguyên của tham số m để phương trình sin x + ( m - 1 ) cos x = 2 m - 1 có nghiệm là
A. 0
B. 3
C. 2
D. 1