Làm câu 9.10.11 thôi ạ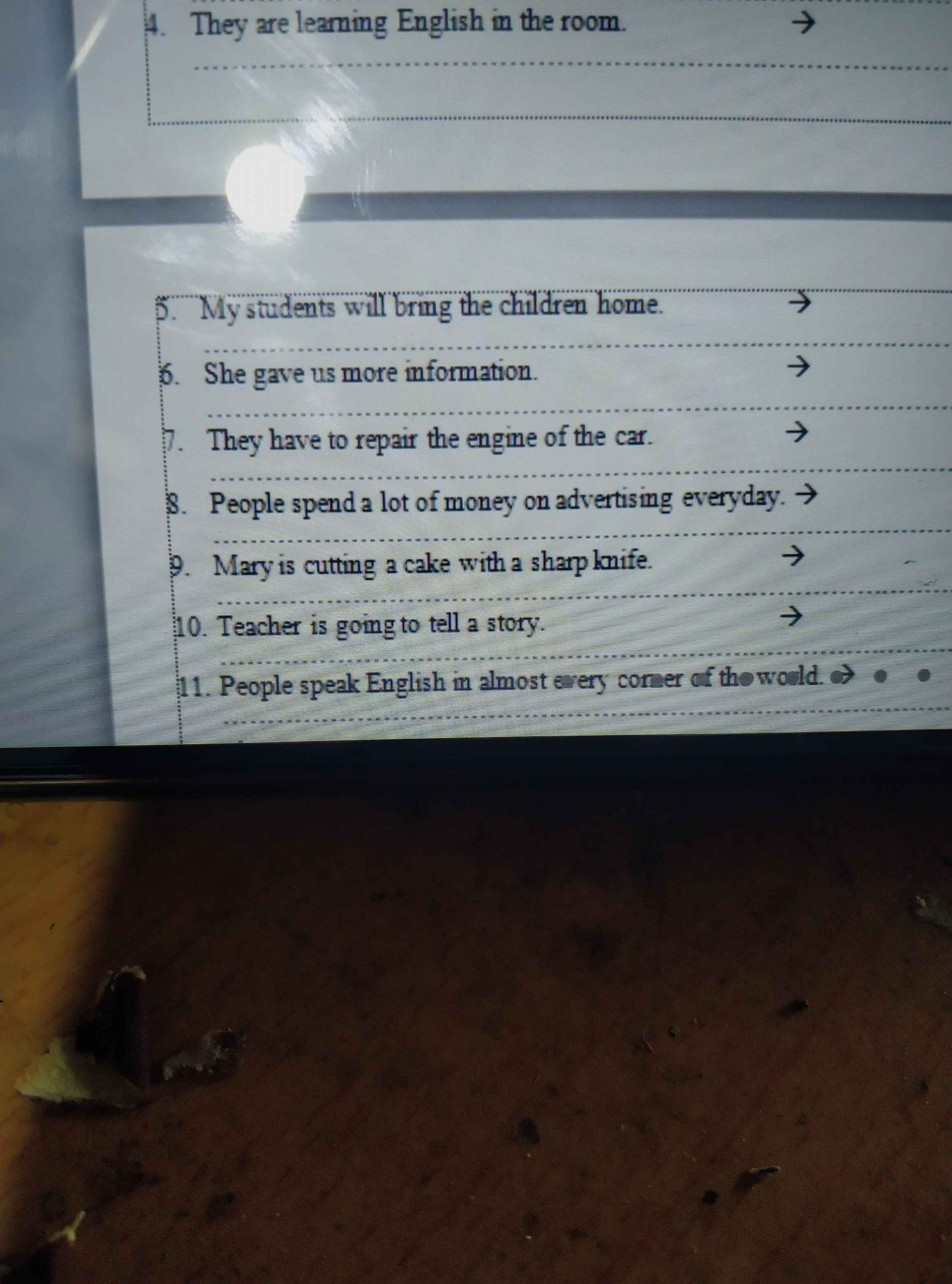

Những câu hỏi liên quan
Câu d thôi ạ, câu a, b, c làm rồi ạ
Gấp ạ!!! Làm câu c thôi ạ
c: Ta có: AM//BC
AE⊥BC
Do đó:AM⊥AE
Suy ra: \(\widehat{AME}+\widehat{AEM}=90^0\)
hay \(\widehat{AME}+\widehat{BAD}=90^0\)
Đúng 0
Bình luận (0)
câu a thôi ạ, câu b làm rồi
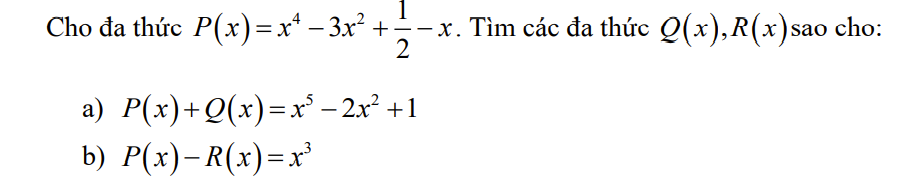
`a)P(x)+Q(x)=x^5-2x^2+1`
`=>Q(x)=x^5-2x^2+1-P(x)`
`=>Q(x)=x^5-2x^2+1-x^4+3x^2-1/2+x`
`=>Q(x)=x^5-x^4+x^2+x+1/2`
______________________________________________
`b)P(x)-R(x)=x^3`
`=>R(x)=P(x)-x^3`
`=>R(x)=x^4-3x^2+1/2-x-x^3`
`=>R(x)=x^4-x^3-3x^2-x+1/2`
Đúng 5
Bình luận (0)
Ta có:
\(P\left(x\right)+Q\left(x\right)=x^5-2x^2+1\)
\(\Rightarrow Q\left(x\right)=P\left(x\right)-\left(x^5-2x^2+1\right)\)
\(=x^4-3x^2+\dfrac{1}{2}-x-x^5+2x^2-1\)
\(=-x^5+x^4-x^2-x-\dfrac{1}{2}\)
Vậy \(Q\left(x\right)=-5^2+x^4-x^2-x-\dfrac{1}{2}\)
Đúng 4
Bình luận (1)
a) <=> Q(x) = (x5 - 2x2 + 1) - P(x)
= (x5 - 2x2 + 1) - (x4 - 3x2 + 1/2 - x)
= x5 - 2x2 + 1 - x4 + 3x2 + x - 1/2
= x5 - x4 + x2 + x + 1/2
Vậy Q(x) = x5 - x4 + x2 + x + 1/2
Đúng 1
Bình luận (0)
Giúp e làm các câu đó đi ạ trừ câu 3, 4 ra thôi ạ


Làm giúp em câu 1 , câu 2 thôi ạ !!
1 The gymnast won a total of ten medals at 3 Olympic Games
2 The principal invited a sports star to give a talk at my school yesterday
Đúng 2
Bình luận (2)
Làm câu c thôi ạ
Làm câu 2,3 thôi ạ
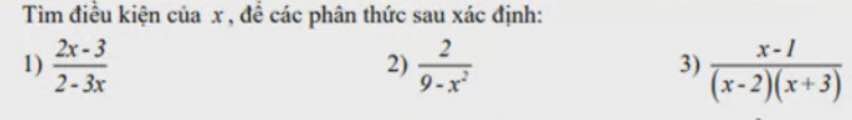
2: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
3: ĐKXĐ: \(x\notin\left\{2;-3\right\}\)
Đúng 1
Bình luận (0)
Làm câu 2 thôi ạ

Bạn tự làm tóm tắt nhé!
a. Ý nghĩa:
Điện trở định mức của biến trở con chạy là 40\(\Omega\)
Cường độ dòng điện định mức của biến trở con chạy là 0,5A
b. Hiệu điện thế lớn nhất mà biến trở chịu được: \(U=R.I=40.0,5=20V\)
c. Tiết diện của dây: \(S=\dfrac{p.l}{R}=\dfrac{0,5.10^{-6}.8}{40}=1,25.10^{-8}m^2\)
Đúng 3
Bình luận (5)

làm câu b thôi ạ
a. Mạch bổ sung:
\(\left[{}\begin{matrix}1:-A-T-G-X-X-G-A-X-G-\\2:-T-A-X-G-G-X-T-G-X-\end{matrix}\right.\)
Đúng 1
Bình luận (1)



















