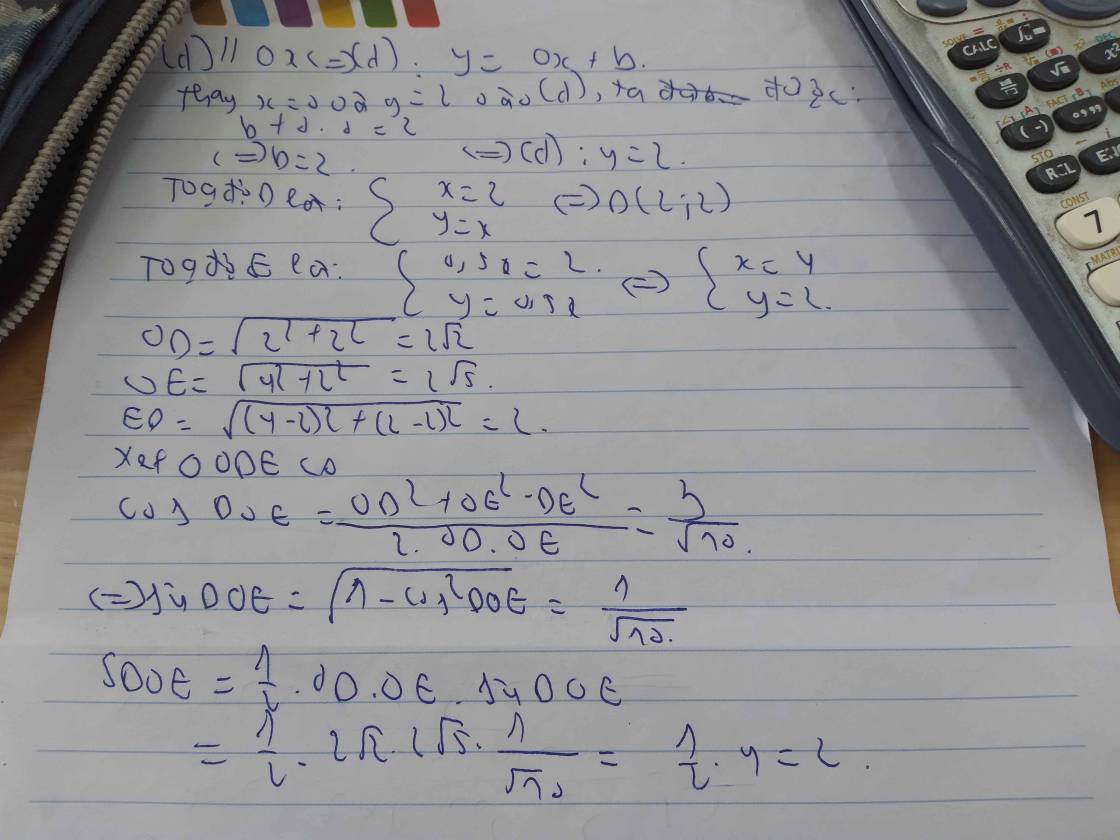Viết pt đg thẳng (d₁) // (d) cắt Ox tại A, Oy tại B và S_∆AOB = 8

Gọi (d₂) có dạng y = ax + b và (d₂) // (d) \(\Rightarrow y=4x+b\)

A có tọa độ = (a;0) \(\Rightarrow O_A=\left|a\right|=4\)

B có tọa độ = (b;0) \(\Rightarrow O_B=\left|b\right|\)

Lại có \(\frac{1}{2}\left|ab\right|=8\Rightarrow\frac{1}{2}.4.\left|b\right|=8\Rightarrow\orbr{\begin{cases}b=4\\b=-4\end{cases}}\)

a: Đặt (d1): y=ax+b(a<>0)

Vì (d1) vuông góc với (d) nên 3a=-1

=>\(a=-\dfrac{1}{3}\)

Vậy: (d1): \(y=-\dfrac{1}{3}x+b\)

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x=-b\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\\dfrac{x}{3}=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3b\\y=0\end{matrix}\right.\)

=>A(3b;0)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{3}\cdot0+b=b\end{matrix}\right.\)

=>B(0;b)

\(AB=2\sqrt{10}\)

=>\(AB^2=40\)

=>\(\left(0-3b\right)^2+\left(b-0\right)^2=40\)

=>\(10b^2=40\)

=>\(b^2=4\)

=>b=2 hoặc b=-2

Vậy: (d1): y=-1/3x+2 hoặc (d1): y=-1/3x-2

b: Đặt (d2): y=ax+b

Vì (d2)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-5\end{matrix}\right.\)

Vậy: (d2): y=3x+b

Tọa độ C là:

\(\left\{{}\begin{matrix}y=0\\3x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{b}{3}\end{matrix}\right.\)

=>\(C\left(-\dfrac{b}{3};0\right)\)

tọa độ D là:

\(\left\{{}\begin{matrix}x=0\\y=3x+b=3\cdot0+b=b\end{matrix}\right.\)

=>D(0;b)

\(OC=\sqrt{\left(-\dfrac{b}{3}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{b}{3}\right)^2+0}=\dfrac{\left|b\right|}{3}\)

\(OD=\sqrt{\left(0-0\right)^2+\left(b-0\right)^2}=\sqrt{0^2+b^2}=\left|b\right|\)

Vì Ox\(\perp\)Oy nên OC\(\perp\)OD

=>ΔOCD vuông tại O

=>\(S_{OCD}=\dfrac{1}{2}\cdot OC\cdot OD\)

=>\(S_{OCD}=\dfrac{\dfrac{1}{2}\left|b\right|}{3}\cdot\left|b\right|=\dfrac{1}{2}\cdot\dfrac{b^2}{3}\)

Để \(S_{OCD}=6\) thì \(\dfrac{b^2}{6}=6\)

=>\(b^2=36\)

=>\(b=\pm6\)

Vậy: (d2): y=3x+6 hoặc (d2): y=3x-6

Để ΔOCD cân tại O thì OC=OD

=>\(\dfrac{\left|b\right|}{3}=\left|b\right|\)

=>\(\left|b\right|=0\)

=>b=0

Vậy: (d2): y=3x

a: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m+1=-\dfrac{1}{2}\\-5< >3\left(đúng\right)\end{matrix}\right.\)

=>\(m+1=-\dfrac{1}{2}\)

=>\(m=-\dfrac{3}{2}\)

b: Thay x=2 vào y=x+3, ta được:

\(y=2+3=5\)

Thay x=2 và y=5 vào (d), ta được:

\(2\left(m+1\right)-5=5\)

=>2(m+1)=10

=>m+1=5

=>m=5-1=4

c: Tọa độ A là:

\(\left\{{}\begin{matrix}x=0\\y=\left(m+1\right)x-5=0\cdot\left(m+1\right)-5=-5\end{matrix}\right.\)

=>A(0;-5)

\(OA=\sqrt{\left(0-0\right)^2+\left(-5-0\right)^2}=\sqrt{0^2+5^2}=5\)

Tọa độ B là:

\(\left\{{}\begin{matrix}\left(m+1\right)x-5=0\\y=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\left(m+1\right)x=5\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{m+1}\\y=0\end{matrix}\right.\)

=>\(B\left(\dfrac{5}{m+1};0\right)\)

\(OB=\sqrt{\left(\dfrac{5}{m+1}-0\right)^2+\left(0-0\right)^2}\)

\(=\sqrt{\left(\dfrac{5}{m+1}\right)^2}=\dfrac{5}{\left|m+1\right|}\)

Ox\(\perp\)Oy

=>OA\(\perp\)OB

=>ΔOAB vuông tại O

ΔOAB vuông tại O

=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot5\cdot\dfrac{5}{\left|m+1\right|}=\dfrac{25}{2\left|m+1\right|}\)

Để \(S_{AOB}=5\) thì \(\dfrac{25}{2\left|m+1\right|}=5\)

=>\(2\left|m+1\right|=5\)

=>|m+1|=5/2

=>\(\left[{}\begin{matrix}m+1=\dfrac{5}{2}\\m+1=-\dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)

b: Để hai đường song song thì m-2=2

=>m=4

c: Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\x=\dfrac{-2}{m-2}\end{matrix}\right.\Leftrightarrow OA=\dfrac{2}{\left|m-2\right|}\)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Leftrightarrow OB=2\)

S_AOB=1

=>1/2*4/|m-2|=1

=>4/|m-2|=2

=>|m-2|=2

=>m=4 hoặc m=0