cho tam giác abc vuông tại a .Vẽ đường cao AH.Kẻ AM là tia pg của góc HAC .a,CMR tam giác AHM=tam giác AKM.b, gọi I là giao điểm của HA và MK.CM tam giác AKI= tam giác AHC .c, CM tam giác MAI= tam giác MAC .d, tam giác IMC cân.e,AM vuông góc với IC

Những câu hỏi liên quan
B1: Cho tam giác ABC có góc C bằng 30 độ. Tia phân giác của góc B và đường phân giác góc ngoài tại A cắt nhau ở E. Tính số đo góc BCEB2: Cho tam giác ABC có I là giao điểm các tia pg của góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc BC (H thuộc BC) CMR: góc BIH góc CIDB3: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. (H thuộc BC), các tia pg của góc HAC và AHC cắt nhau ở I. Tia phân giác của góc HAB cắt BC ở D. Cm: CI điq ua trung điểm của AD
Đọc tiếp
B1: Cho tam giác ABC có góc C bằng 30 độ. Tia phân giác của góc B và đường phân giác góc ngoài tại A cắt nhau ở E. Tính số đo góc BCE
B2: Cho tam giác ABC có I là giao điểm các tia pg của góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc BC (H thuộc BC) CMR: góc BIH = góc CID
B3: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. (H thuộc BC), các tia pg của góc HAC và AHC cắt nhau ở I. Tia phân giác của góc HAB cắt BC ở D. Cm: CI điq ua trung điểm của AD
Cho tam giác ABC cân tại A. Điểm H là trung điểm của cạnh BC.
a) CM tam giác AHB = tam giác AHC. CM AH vuông góc với BC.
b) Kẻ HM vuông góc với AB tại M, kẻ HN vuông góc với AC tại N. CM tam giác AHM = tam giác AHN.
c) Gọi I là giao điểm của MH và AC, gọi K là giao điểm của NH và AB. CM tam giác AIK là tam giác cân.
a) Xét \(\Delta AHB\)và\(\Delta AHC\)có :
\(\hept{\begin{cases}HB=HC\\AH\\AB=AC\end{cases}}\)( Bạn tự ghi lời giải thích nha)
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}\)(2 cạnh tương ứng)
Mà \(\widehat{AHB}+\widehat{AHC}=180^o\)( 2 góc kề bù )
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AH\perp BC\)
b) Xét \(\Delta AHM\left(\widehat{AMH}=90^o\right)\)và \(\Delta AHN\left(\widehat{ANH}=90^o\right)\)có :
\(\hept{\begin{cases}AH\\\widehat{A_1}=\widehat{A_2}\end{cases}}\)( bạn tự nêu lí do )
\(\Rightarrow\Delta AHM=\Delta AHN\)( Cạnh huyền - góc nhọn )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB AC.Vẽ đường cao AH của tam giác ABC,AD là tia phân giác góc HAC ( D thuộc HC).Vẽ DE vuông góc AC tại Ea) CMR : Tam giác ADH tam giác ADE Từ đó DH DEb) Gọi K là giao điểm AH và D.CMRTam giác DKC cânc) Gọi F là trug điểm KC.CMR : A,D,F thẳng hàngd)CMR : AH + BC AB + ACe) Gọi I là trực tâm Của tam giác BAD.ĐƯờng thẳng vuông góc với AD tại A cắt phân giác góc IDB tại T.CMR tam giác ADT là tam vuông cânMn giảng giúp em câu e với ạ
Đọc tiếp
Cho tam giác ABC vuông tại A có AB < AC.Vẽ đường cao AH của tam giác ABC,AD là tia phân giác góc HAC ( D thuộc HC).Vẽ DE vuông góc AC tại E
a) CMR : Tam giác ADH = tam giác ADE Từ đó => DH = DE
b) Gọi K là giao điểm AH và D.CMRTam giác DKC cân
c) Gọi F là trug điểm KC.CMR : A,D,F thẳng hàng
d)CMR : AH + BC > AB + AC
e) Gọi I là trực tâm Của tam giác BAD.ĐƯờng thẳng vuông góc với AD tại A cắt phân giác góc IDB tại T.CMR tam giác ADT là tam vuông cân
Mn giảng giúp em câu e với ạ
e: I là trực tâm của ΔBAD
=>DI vuông góc AB
=>DI//AC
=>góc BDI=góc ACB
DT là phân giác của góc IDB
=>góc TDI=góc TDB=1/2*góc BDI=1/2*góc ACB
DI//AC
=>góc IDA=góc DAC
AD là phân giác của góc HAC
=>góc DAC=1/2*góc HAC
=>góc IDA=1/2*góc HAC
góc HAC+góc ACB=90 độ
=>góc IDT+góc IDA=1/2*90=45 độ
=>góc TDA=45 độ
=>ΔTDA vuông cân
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A,đường cao AH.Kẻ HK vuông góc với AC tại K
a)CM:tam giác ABC đồng dạng tam giác HAC;tam giác AHB đồng dạng tam giác HKA
b)CM: AH^2=HK.AB
c)Gọi M là trung điểm của AB,đoạn CM cắt HK tại I.Cm:I là trung điểm của HK
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
Xét ΔAHB vuông tại H và ΔHKA vuông tại K có
góc HAB=góc KHA
=>ΔAHB đồng dạng với ΔHKA
b: ΔAHB đồng dạng với ΔHKA
=>AH/HK=AB/HA
=>AH^2=HK*AB
c: Xét ΔCAM có KI//AM
nên KI/AM=CI/CM
Xét ΔCMB có IH//MB
nên IH/MB=CI/CM
=>KI/AM=IH/MB
mà AM=MB
nên KI=IH
=>I là trung điểm của KH
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, gọi H là trung điểm của BC. Chứng minh:
a/ Tam giác ABC = tam giác AHC.
b/ AH là tia phân giác của góc A và AH vuông góc BC.
c/ Từ H vẽ HM vuông góc AB, HN vuông góc AC. Chứng minh tam giác AHM = tam giác AHN từ đó suy ra tam giác HMN cân.
Xem chi tiết
Câu a bạn có chép sai ko vậy?
Đúng 0
Bình luận (0)
Giải
b)Xét tam giác BAH và CAH có:
AB=AC(gt)
góc B =góc C(gt)
AH chung
\(\Rightarrow\)tam giác BAH =CAH (c.g.c)
\(\Rightarrow\)góc BAH=CAH (2 góc t/ư)
Mặt khác AH nằm giữa AB và AC ,chia góc A thành 2 góc bằng nhau
Mà H là trung điểm BC
\(\Rightarrow\)AH là tia phân giác góc A và vuông góc BC
Đúng 0
Bình luận (0)
a) Sửa đề: ΔAHB=ΔAHC
Xét ΔAHB và ΔAHC có
AH chung
AB=AC(ΔABC cân tại A)
HB=HC(H là trung điểm của BC)
Do đó: ΔAHB=ΔAHC(c-g-c)
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A có AB AC.Vẽ đường cao AH của tam giác ABC,AD là tia phân giác góc HAC ( D thuộc HC).Vẽ DE vuông góc AC tại Ea) CMR : Tam giác ADH tam giác ADE Từ đó DH DEb) Gọi K là giao điểm AH và D.CMRTam giác DKC cânc) Gọi F là trug điểm KC.CMR : A,D,F thẳng hàngd)CMR : AH + BC AB + ACe) Gọi I là trực tâm Của tam giác BAD.ĐƯờng thẳng vuông góc với AD tại A cắt phân giác góc IDB tại T.CMR tam giác ADT là tam vuông cân
Đọc tiếp
Cho tam giác ABC vuông tại A có AB < AC.Vẽ đường cao AH của tam giác ABC,AD là tia phân giác góc HAC ( D thuộc HC).Vẽ DE vuông góc AC tại E
a) CMR : Tam giác ADH = tam giác ADE Từ đó => DH = DE
b) Gọi K là giao điểm AH và D.CMRTam giác DKC cân
c) Gọi F là trug điểm KC.CMR : A,D,F thẳng hàng
d)CMR : AH + BC > AB + AC
e) Gọi I là trực tâm Của tam giác BAD.ĐƯờng thẳng vuông góc với AD tại A cắt phân giác góc IDB tại T.CMR tam giác ADT là tam vuông cân
Bài 5.Cho tam giác ABC vuông tại A, (AB < AC), đường cao AH. AD là tia phân giác của tam giác AHC, kẻ DE vuông góc AC tại E.
CMR: a)tam giác AHD = tam giác AED
b) tam giác BAD cân;
c) Gọi K là giao điểm của DE và AH. Chứng minh: tam giác HDK = tam giác EDC;
d) AD vuông góc CK
e) HE // KC;
giải giúp mik với ạ. ai làm được mik tick luôn
Đúng 0
Bình luận (0)
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
\(\widehat{HAD}=\widehat{EAD}\)
Do đó: ΔAHD=ΔAED
b: Ta có: \(\widehat{BAD}+\widehat{CAD}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)
mà \(\widehat{CAD}=\widehat{HAD}\)
nên \(\widehat{BAD}=\widehat{BDA}\)
Xét ΔABD có \(\widehat{BAD}=\widehat{BDA}\)
nên ΔBAD cân tại B
c: Xét ΔHDK vuông tại H và ΔEDC vuông tại E có
DH=DE
\(\widehat{HDK}=\widehat{EDC}\)
Do đó: ΔHDK=ΔEDC
Đúng 0
Bình luận (0)
bạn học thcs thị trấn văn điển lớp 8a1 cô hằng nhỉ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A. Vẽ đường cao AH
a) Cm tam giác HBA và tam giác ABC đồng dạng và AB² = HB.BC
b) Vẽ đường phân giác CD của Tam giác ABC. Từ B vẽ BK vuông góc CD tại K, gọi I là giao điểm của AH và CD. Cm KD.HC=KB.HI
c) Gọi E là giao điểm của AH và BK. Trên CD lấy điểm F sao cho BA=BF. Cm BF vuông góc EF
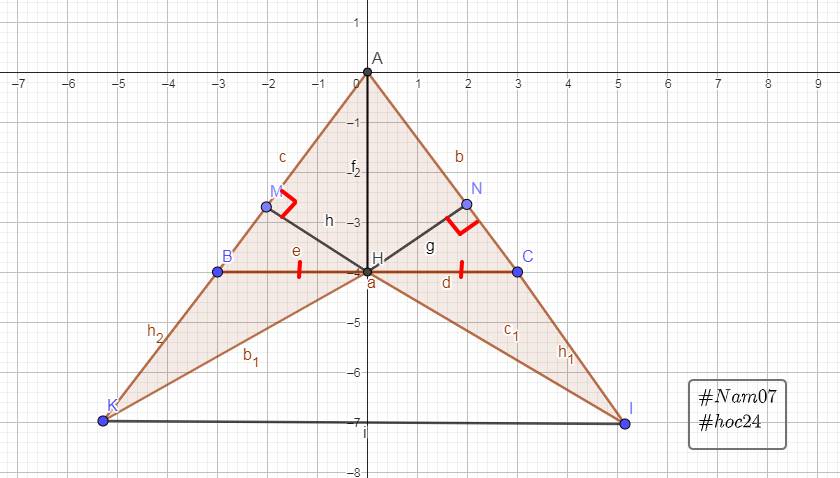
tam giác ABC cân tại A,H là trung điểm của BC
a.Chứng minh tam giác ABH =tam giác AHC và AH vuông góc với BC
b,kẻ HM vuông góc với AC tại M, kẻ HN vuông góc với AC tại N.Chứng minh tam giác AHM=Tam giác AHN
c. Gọi I là giao điểm của MH và AC,K là giao điểm của NH và AB. Chứng minh tam giác AIK là tam giác cân
`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.
Đúng 1
Bình luận (0)

















