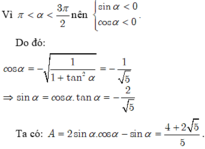Cho góc nhọn α , tính giá trị của biểu thức
A=(3sinα+4cosα)2 + ( 4sinα-3cosα)2

Những câu hỏi liên quan
Cho tan
α
2. Tính giá trị của biểu thức:
G
2
sin
α
+
cos
α
cos
α
−
3
sin
α
A. G 1 B. G
−
4
5
C. G
−
6
5...
Đọc tiếp
Cho tan α = 2. Tính giá trị của biểu thức: G = 2 sin α + cos α cos α − 3 sin α
A. G = 1
B. G = − 4 5
C. G = − 6 5
D. G = −1
Vì tan α = 2 nên cos α ≠ 0
Ta có: G = 2 sin α + cos α cos α − 3 sin α = 2 sin α cos α + cos α sin α cos α cos α − 3 sin α cos α = 2 tan α + 1 1 − 3 tan α
Thay tan α = 2 ta được: G = 2.2 + 1 1 − 3.2 = − 5 5 = − 1
Vậy G = −1
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho góc nhọn α, tính giá trị lớn nhất của P = 2sinα + 3cosα
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2=(2\sin a+3\cos a)^2\leq (2^2+3^2)(\sin ^2a+\cos ^2a)=13$
$\Rightarrow P\leq \sqrt{13}$
Vậy $P_{\max}=\sqrt{13}$
Giá trị này đạt tại $\frac{\sin a}{2}=\frac{\cos a}{3}$
Đúng 1
Bình luận (1)
Cho tan
α
4. Tính giá trị của biểu thức
P
3
sin
α
−
5
cos
α
4
cos
α
+
sin
α
A. P
7
8
B. P
17
8...
Đọc tiếp
Cho tan α = 4. Tính giá trị của biểu thức P = 3 sin α − 5 cos α 4 cos α + sin α
A. P = 7 8
B. P = 17 8
C. P = 8 7
D. P = 5 8
Vì tan α = 2 nên cos α ≠ 0 , chia cả tử và mẫu của P cho cos α ta được:
Ta có: P = 3 sin α − 5 cos α 4 cos α + sin α = 3 sin α cos α − 5 cos α cos α 4 cos α cos α + sin α cos α = 3. tan α − 5 4 + tan α
Thay tan α = 4 ta được: P = 3.4 − 5 4 + 4 = 7 8
Vậy P = 7 8
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho góc nhọn α. Giá trị của biểu thức
P
s
i
n
2
90
°
−
α
+
s
i
n
2
α
là A.1 B. 2 C.
2
s
i
n
2
90
°
−
α
D.
2
s
i
n...
Đọc tiếp
Cho góc nhọn α. Giá trị của biểu thức P = s i n 2 90 ° − α + s i n 2 α là
A.1
B. 2
C. 2 s i n 2 90 ° − α
D. 2 s i n 2 α
Đáp án A
P = s i n 2 90 ° − α + s i n 2 α = c o s 2 α + s i n 2 α = 1
Đúng 0
Bình luận (0)
~Các bạn giúp mk làm bài này nhé! Cảm ơn các bạn nhiều ...~ Bài 1:Tính giá trị biểu thứca) A sin10°+sin20°+sin30°+sin40°-cos50°-cos60°-cos70°-cos80°b) C cos²52° sin45°+sin²52° cos45°c) E sin²5°+sin²15°+sinv25°+sin²35°+sin²45°+sin²55°+sin²65°+sin²75°+sin²85°Bài 2: C/m rằng với góc nhọn α ta luôn cóa) (sinα +cosα)²-(sinα -cosα)² 4sinα cosαb) cosα/1-sinα 1+sinα/cosαc) √̅s̅i̅n̅²̅x̅(̅1̅+̅̅c̅o̅t̅̅x̅)̅̅+̅c̅o̅s̅²̅x̅(̅1̅+̅t̅a̅n̅x̅)̅ sinx+cosxBài 3: Cho α là một góc nhọn a) Biết sinα 3/4. Tính cosα(90°-...
Đọc tiếp
~Các bạn giúp mk làm bài này nhé! Cảm ơn các bạn nhiều ...~
Bài 1:Tính giá trị biểu thức
a) A= sin10°+sin20°+sin30°+sin40°-cos50°-cos60°-cos70°-cos80°
b) C= cos²52° sin45°+sin²52° cos45°
c) E= sin²5°+sin²15°+sinv25°+sin²35°+sin²45°+sin²55°+sin²65°+sin²75°+sin²85°
Bài 2: C/m rằng với góc nhọn α ta luôn có
a) (sinα +cosα)²-(sinα -cosα)² = 4sinα cosα
b) cosα/1-sinα =1+sinα/cosα
c) √̅s̅i̅n̅²̅x̅(̅1̅+̅̅c̅o̅t̅̅x̅)̅̅+̅c̅o̅s̅²̅x̅(̅1̅+̅t̅a̅n̅x̅)̅ =sinx+cosx
Bài 3: Cho α là một góc nhọn
a) Biết sinα =3/4. Tính cosα(90°-α)
b) Biết tanα =2. Tính cotα(90°-α)
Cho góc
α
thỏa mãn
π
α
3
π
2
và
tan
α
2
: Tính giá trị của biểu thức
A
sin
2
α
+
cos
α
+
π
2
A.
4
+
2
5
10...
Đọc tiếp
Cho góc α thỏa mãn π < α < 3 π 2 và tan α = 2 : Tính giá trị của biểu thức A = sin 2 α + cos α + π 2
A. 4 + 2 5 10
B. 4 + 5 5 5
C. 4 + 2 5 5
D. 2 + 5 5
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trịcủa các góc nhọn α.a) A cos4α + 2cos2α . sin2α + sin4ab) B sin4α + cos2α . sin2α + cos2αc) C 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos αd) D (tan α - cot α )2 - (tan α + cot α )2e) E 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)f) F dfrac{1}{1+sintext{α}}+dfrac{1}{1-sintext{α}}-2 tan2α
Đọc tiếp
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị
của các góc nhọn α.
a) A = cos4α + 2cos2α . sin2α + sin4a
b) B = sin4α + cos2α . sin2α + cos2α
c) C = 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos α
d) D = (tan α - cot α )2 - (tan α + cot α )2
e) E = 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)
f) F = \(\dfrac{1}{1+sin\text{α}}\)+\(\dfrac{1}{1-sin\text{α}}\)-2 tan2α
Câu 50**: Cho góc nhọn α tuỳ ý giá trị biểu thức dfrac{tanalpha}{cotalpha}+dfrac{cotalpha}{tanalpha}-dfrac{sin^2alpha}{cos^2alpha}bằng A. tan^2alpha ; B . cot^2 α ; C . 0 ; D. 1 .giải hộ mik vs
Đọc tiếp
Câu 50**: Cho góc nhọn α tuỳ ý giá trị biểu thức \(\dfrac{tan\alpha}{cot\alpha}+\dfrac{cot\alpha}{tan\alpha}-\dfrac{sin^2\alpha}{cos^2\alpha}\)bằng
A. \(tan^2\alpha\) ; B . \(cot^2\) α ; C . 0 ; D. 1 .
giải hộ mik vs
Cho góc α thỏa mãn tanα 2. Tính
P
3
sin
α
-
2
cos
α
5
cos
α
+
7
sin
α
A. P -4/9 B. P 4/9 C. P -4/19 D. P 4/19
Đọc tiếp
Cho góc α thỏa mãn tanα = 2. Tính P = 3 sin α - 2 cos α 5 cos α + 7 sin α
A. P = -4/9
B. P = 4/9
C. P = -4/19
D. P = 4/19
Chọn D.
Chia cả tử và mẫu của biểu thức P cho cosα ta được
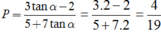
Đúng 0
Bình luận (0)
với α là góc nhọn tim giá trị lớn nhất của biểu thức sinα +sin (90 0 - α )
Đặt \(A=sin\alpha+sin\left(90^0-\alpha\right)=sin\alpha+cos\alpha\)
\(\Rightarrow A^2=\left(sin\alpha+cos\alpha\right)^2\le2\left(sin^2\alpha+cos^2\alpha\right)=2\)
\(\Rightarrow A\le\sqrt{2}\)
\(A_{max}=\sqrt{2}\) khi \(\alpha=45^0\)
Đúng 4
Bình luận (0)