I2-xI+2=x
Ix-1I-x+1=0
Ix-1I=I2-xI
giải phương trình
I x-1I + I2-xI=3
Tìm x:
a,I2xI=3-x
b,Ix-1I=2x-1
c,I9-xI-9=3x
d,I3x-1I+2=x
e,I3x-5I+x=2
a) \(\left|2x\right|=3-x\)
\(\Rightarrow\orbr{\begin{cases}2x=3-x\\2x=x-3\end{cases}}\Rightarrow\orbr{\begin{cases}2x+x=3\\2x-x=-3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}3x=3\\x=-3\end{cases}}\Rightarrow\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)
b) \(\left|x-1\right|=2x-1\)
\(\Rightarrow\orbr{\begin{cases}x-1=2x-1\\x-1=1-2x\end{cases}}\Rightarrow\orbr{\begin{cases}x-2x=-1+1\\x+2x=1+1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}-x=0\\3x=2\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{2}{3}\end{cases}}\)
Mình làm mẫu câu a) nhé
Do |2x|>hoặc =0
=>3-x.hoặc =0
=>x<hoặc =3 (1)
Mà |2x| chẵn với mọi x
=>3-x là số chẵn
=>x lẻ (2)
Từ (1) và (2) ta có :
x thuộc {1;3}
+Nếu x=1=>|2x|=2
3-x=2 (t/mãn)
+Nếu x=3=>|2x|=6
3-x=0 (loại)
Vậy x =1
Giá trị của tổng 1 + 1 i + 1 i 2 + . . . + 1 i 2019 ( ở đó i 2 = - 1 ) bằng
A. 0
B. 1
C. -1
D. i
Chọn A.
Gọi S là tổng cần tính. Áp dụng công thức tính tổng của cấp số nhân ta có
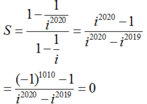
Tìm x :
I x-1I - 2 I1-xI = -5
| x-1 | -2 |1-x| =-5
|x-1| -2 |x-1|=-5
|x-1| (1-2)=-5
-|x-1|=-5
|x-1|=5
x-1=5 hoac x-1=-5
x=6 x=-4
vay x=6 hoac x=-4
Tập hợp các giá trị của x thỏa mãn Ix + 1I + I1 - xI = 2 là {........}
x = {3, 4 , 4,6,7,8,9,10,.....}
li-ke mình nhé
Bài 1 : lập bảng xét dấu để bỏ giá trị tuyệt đối .
A ) I3x-1I + Ix-1I = 4
C ) I x-2I + Ix-3I + Ix-4I = 2
D ) 2 x Ix+2I + I4-xI = 11
Làm mẫu 1 phần :
a) \(|3x-1|+|x-1|=4\left(1\right)\)
Ta có: \(3x-1=0\Leftrightarrow x=\frac{1}{3}\)
\(x-1=0\Leftrightarrow x=1\)
Lập bảng xét dấu :
+) Với \(x< \frac{1}{3}\Rightarrow\hept{\begin{cases}3x-1< 0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|3x-1|=1-3x\\|x-1|=1-x\end{cases}\left(2\right)}}\)
Thay (2) vào (1) ta được :
\(\left(1-3x\right)+\left(1-x\right)=4\)
\(2-4x=4\)
\(4x=-2\)
\(x=\frac{-1}{2}\)( chọn )
+) Với \(\frac{1}{3}\le x< 1\Rightarrow\hept{\begin{cases}3x-1>0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|3x-1|=3x-1\\|x-1|=1-x\end{cases}\left(3\right)}}\)
Thay (3) vào (1) ta được :
\(\left(3x-1\right)+\left(1-x\right)=4\)
\(2x=4\)
\(x=2\)( chọn )
+) Với \(x\ge1\Rightarrow\hept{\begin{cases}3x-1>0\\x-1>0\end{cases}\Rightarrow}\hept{\begin{cases}|3x-1|=3x-1\\|x-1|=x-1\end{cases}\left(4\right)}\)
Thay (4) vào (1) ta được :
\(\left(3x-1\right)+\left(x-1\right)=4\)
\(4x-2=4\)
\(4x=6\)
\(x=\frac{3}{2}\)( chọn )
Vậy \(x\in\left\{\frac{-1}{2};2;\frac{3}{2}\right\}\)
Tìm x thỏa mãn:
lx-1I+I1-xI=4-x
Ix-1I và I1-xI là 2 số đối nhau nên tổng của chúng luôn =0 với mọi x.
=> 4-x=0 => x=4
Đs: x=4
bài 1 ; tìm x
a,2x+1=3x-5
b,2.(x-2)=5x-1/2
c,Ix-1I=1/2
d,I2-3xI+1/2=2/3
e,1/2x-2/3=1/4
j,3.(2x-1)=x-2
g,I1/2x-1I=1/3
h,I3x-2I-1/2=1
CẢM ƠN NHÉ
a, 2x+1=3x-5
1=x-5(giảm cả hai vế đi 2x)
1+5=x
x=6
b,2.(x.2)=5x-1/2
2.2.x=5x-1/2
4x=5x-1/2
4x+1/2=5x(giảm cả hai vế đi 4x)
1/2=x
c,lx-1l=1/2
lxl=1/2+1
lxl=1,5
x=1,5;-1,5
d,I2-3xI+1/2=2/3
l2-3xl=2/3-1/2
l2-3xl=1/3
l3xl=2-1/3
l3xl=5/3
lxl=5/3:3
lxl=5/9
x=5/9;-5/9
e,1/2x-2/3=1/4
1/2x=1/4+2/3
1/2x=11/12
x=11/12:1/2
x=11/6
j,3.(2x-1)=x-2
6x-3=x-2
6x-1=x
1=6x-x
1=5x
x=1/5
g,I1/2x-1I=1/3
l1/2xl=1/3+1
l1/2xl=4/3
lxl=4/3:1/2
lxl=8/3
x=8/3;-8/3
h,I3x-2I-1/2=1
l3x-2l=1+1/2
l3x-2l=3/2
l3xl=3/2+2
l3xl=7/2
lxl=7/2:3
lxl=7/6
x=7/6;-7/6
Ix-1I+I3-xI =6/Iy+3I +3
Ta có: \(\left\vert x-1\right\vert+\left\vert3-x\right\vert\ge\left\vert x-1+3-x\right\vert=2\forall x\)
\(\left|y+3\right|\ge0\forall y\)
=>\(\left\vert y+3\right\vert+3\ge3\forall y\)
=>\(\frac{6}{\left|y+3\right|+3}\le\frac63=2\forall y\)
mà \(\frac{6}{\left\vert y+3\right\vert+3}=\left\vert x-1\right\vert+\left\vert3-x\right\vert\)
nên dấu '=' xảy ra khi y+3=0 và (x-1)(3-x)>=0
=>y=-3 và (x-1)(x-3)<=0
=>y=-3 và 1<=x<=3