Trả lời :

vì AB//DC(gt) suy ra AB//DE

và AC//BE(gt)

do hai đoạn thẳng song song(AB//DE) chắn bởi 2 đường thẳng song song (AC//BE) suy ra AC=BE

Mà AC=BD(gt)

suy ra BD=BE

Trong tam giác BDE có BD=BE suy ra tam giác BDE cân tại B (dpcm)

a: Xét ΔACB và ΔEBC có

\(\widehat{ABC}=\widehat{ECB}\)(AB//EC)

BC chung

\(\widehat{ACB}=\widehat{EBC}\)(AC//BE)

Do đó: ΔACB=ΔEBC

b: ΔACB=ΔEBC

=>AC=BE

mà AC=BD

nên BE=BD

=>ΔBDE cân tại B

c: ΔBDE cân tại B

=>\(\widehat{BDE}=\widehat{BED}\)

=>\(\widehat{BDC}=\widehat{BED}\)

mà \(\widehat{BED}=\widehat{ACD}\)(AC//BE)

nên \(\widehat{ACD}=\widehat{BDC}\)

bạn chịu khó nhìn chữ viết tay nhé

a: Xét tứ giác ABEC có

AB//CE

AC//BE

Do đó: ABEC là hình bình hành

Suy ra: AC=BE

mà AC=BD

nên BE=BD

Xét ΔBDE có BE=BD

nên ΔBDE cân tại B

b: Xét ΔACD và ΔBDC có 

AC=BD

AD=BC

CD chung

Do đó: ΔACD=ΔBDC

c: Hình thang ABCD có AC=BD

nên ABCD là hình thang cân

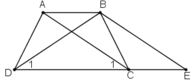
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE     (1)

Theo giả thiết AC = BD     (2)

Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân

Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE     (1)

Theo giả thiết AC = BD     (2)

Từ (1) và (2) suy ra BE = BD do đó  \(\Delta BDE\) cân 

b ) Ta có : AC // BE 

\(\Rightarrow\widehat{C}_1=\widehat{E}\)      ( 3 )

Tam giác BDE cân tại B ( câu a ) nên \(\widehat{D}_1=\widehat{E}\)       ( 4 )

Từ (3 ) và ( 4 ) \(\Rightarrow\widehat{C}_1=\widehat{D}_1\)

Xét \(\Delta ACD\) và \(\Delta BCD\) có AC = CD ( gt )
\(\widehat{C}_1=\widehat{D}_1\left(cmt\right)\)

CD là cạnh chung 

Nên \(\Delta ACD=\Delta BCD\left(c.g.c\right)\)

c ) Vì \(\Delta ACD=\Delta BCD\) ( câu b ) \(\Rightarrow\widehat{ADC}=\widehat{BCD}\)

Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

Chúc bạn học tốt !!!

1) Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau : Cho hình thang ABCD(AB//CD)ABCD(AB//CD) có AC=BDAC=BD. Qua BB kẻ đường thẳng song song với ACAC, cắt đường thẳng DCDC tại EE. Chứng minh rằng: 

a) BDEBDE là tam giác cân. 

b) △ACD=△BDC.△ACD=△BDC.

c) Hình thang ABCDABCD là hình thang cân.

chúc hok tốt , k nha! sai cũng k

a: Xét ΔBAH có BI là phân giác

nên IA/BA=IH/BH

=>IA*BH=BA*IH

b: ΔACB vuông tạiA có AH vuông góc BC

nên BA^2=BH*BC

\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

AH=3*4/5=2,4cm

CH=4^2/5=3,2cm

c: ΔBAC có BD là phân giác

nên DC/DA=BC/BA

=>DC/DA=BA/BH=AI/IH

=>DC*IH=DC*IA