Cho ba đường thẳng aa'; bb'; cc' cắt nhau tại O. Chứng tỏ rằng trong các góc tạo thành có ít nhất một góc nhỏ hơn hoặc bằng 60 độ.

Những câu hỏi liên quan
Cho hình bình hành ABCD . QUA C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành . Gọi AA' , BB' , DD' là các đường vuông góc từ A , B, C tới đường thẳng xy . Chứng minh rằng AA' = BB' + DD'
Cho hình bình hành ABCD. Qua C kẻ đường thẳng Xy chỉ có 1 điểm chung C với hình bình hành. Gọi AA' , BB' , DD' là các đường vuông góc kẻ từ A , B , D đến đường thẳng Xy.
Chứng minh rằng: AA' = BB' + DD'
hình tự vẽ
Gọi giao điểm của AC và BD là O => O là trung điểm của AC, BD => AO=OC;BO=OD
từ điểm O hạ OO' vuông góc với xy tại O' => OO'//DD' (2 góc đồng vị bằng nhau \(\widehat{OO'y}=\widehat{DD'y}=90^o\))
AO=OC;OO'//DD' => OC là đường trung bình của tứ giác BB'DD' => \(OC=\frac{1}{2}\left(BB'+DD'\right)\)(1)
Mặt khác: BO=OD; OO'//AA' (2 góc đồng vị bằng nhau \(\widehat{OO'y}=\widehat{AA'y}=90^o\))
=>OC là đường trung bình của tam giác AA'C => \(OC=\frac{1}{2}AA'\)(2)
Từ (1) và (2) => \(\frac{1}{2}AA'=\frac{1}{2}\left(BB'+DD'\right)\Leftrightarrow AA'=BB'+DD'\)(đpcm)
Đúng 0
Bình luận (0)
ý lộn, đường trung bình của hình thang BB'DD' nhé chứ ai lại nói tứ giác bao giờ
Đúng 0
Bình luận (0)
Mỗi câu sau đây là đúng hay sai?a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước.b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước.c) Có đúng sáu đường thẳng đi qua bốn điểm (phân biệt) cho trước.d) Hai đường thẳng phân biệt thì song song với nhau.e) Hai đường thẳng không cắt nhau thì song song.f) Hai đường thẳng không song song thì cắt nhau.g) Hai đường thẳng không phân biệt thì trùng nhau.h) Ba đường thẳng phân...
Đọc tiếp
Mỗi câu sau đây là đúng hay sai?
a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước.
b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước.
c) Có đúng sáu đường thẳng đi qua bốn điểm (phân biệt) cho trước.
d) Hai đường thẳng phân biệt thì song song với nhau.
e) Hai đường thẳng không cắt nhau thì song song.
f) Hai đường thẳng không song song thì cắt nhau.
g) Hai đường thẳng không phân biệt thì trùng nhau.
h) Ba đường thẳng phân biệt, đôi một cắt nhau thì có đúng 3 giao điểm (phân biệt).
Câu đúng: a) và g).
Câu sai: b), c), d), e), f), h).
Giải thích:
- Câu b sai vì nếu ba điểm( phân biệt) cho trước là ba điểm thẳng hàng thì có đúng 1 đường thẳng đi qua ba điểm đó.
- Câu c sai vì nếu bốn điểm ( phân biệt) cho trước là bốn điểm thẳng hàng thì có đúng 1 đường thẳng đi qua bốn điểm đó.
- Câu d sai vì hai đường thẳng phân biệt có thể song song hoặc cắt nhau.
- Câu e sai vì hai đường thẳng không cắt nhau có thể trùng nhau hoặc song song.
- Câu f sai vì hai đường thẳng không song song có thể có thể trùng nhau hoặc cắt nhau.
- Câu h sai vì ba đường thẳng phân biệt, đôi một cắt nhau thì có thể có đúng 1 giao điểm. Như hình vẽ dưới đây.
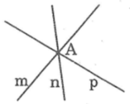
Đúng 0
Bình luận (0)
Cho 101 đường thẳng, trong đó bất cứ hai đường thẳng nào cũng cắt nhau , không có ba đường thẳng nào đồng qui.Số giao điểm của chúng là?
Cho điểm A nằm ngoài đường thẳng d và cách d môt khoảng 2 cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm thuộc tia đối của tia BA sao cho BC = Ba. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?
Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. lấy điểm B bất kì thuộc đường thằng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào ?
Bài giải:
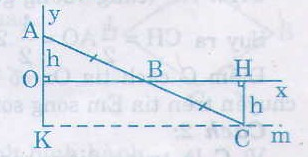
Kẻ AH và CK vuông góc với d.
Ta có AB = CB (gt)
=
( đối đỉnh)
nên ∆AHB = ∆CKB (cạnh huyền - góc nhọn)
Suy ra CK = AH = 2cm
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.
Đúng 0
Bình luận (0)
bn lm sai r. hình sai giải cũng sai
Đúng 0
Bình luận (0)
Cho n đường thẳng trong đó bất kì hai đường thẳng nào cũng cắt nhau.Ko có ba đường thẳng nào đồng quy biết số giao điểm của chúng là 780.Tính n
Cho tam giác ABC có A^=1200. Từ C kẻ đường thẳng song song đường phân giác AD của tam giác ABC, đường thẳng này cắt đường thẳng BA ở M. Tính AMC và ACM
(Hình giống như bài bên kia, khác chỗ A^ = 120o)
BAD^ + DAC^ = BAC^
Mà BAD^ = DAC^
=> BAD^ = DAC^ = BAC^/2 = 120o/2= 60o
Ta có: AD // CM
=> DAC^ = ACM^ = 60o (sole trong)
=> BAD^ = AMC^ = 60o (đồng vị)
Đúng 0
Bình luận (0)
Cho n đường thẳng trong đó bất kì hai đường thẳng nào cũng cắt nhau. Không có ba đường thẳng nào đồng quy biết số giao điểm của chúng là 780.Tính n
Theo đề ra ta có :
\(\frac{n\left(n-1\right)}{2}=780\)
\(\Rightarrow\left(n-1\right)n=1560\)
\(\Rightarrow\left(n-1\right)n=39.40\)
=> n = 39
Vậy có 39 điểm
Đúng 0
Bình luận (0)
cho bốn điểm M , N ,P ,Q trong đó ba điểm M ,N ,P thẳng hàng và điểm Qnằm ngoài đường thẳng trên . Kẻ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thẳng [ phân biệt]? viết tên các đường thẳng đó?
các bạn giúp mình
- Qua ba điểm M,N,P thẳng hàng chỉ có một đường thằng MN.
- Xét điểm Q với mỗi điểm M,N,P ta có ba đường thẳng QM,QN,QP. vậy có 4 đường thẳng là MN, QM,QN,QP.
Đúng 0
Bình luận (0)
bn ơi bài này
vẽ hình lằn nhằng
lắm bn ạ bn cứ
làm như bn cô bé yêu đời
đó nhé
Đúng 0
Bình luận (0)



















