Giải các bất phương trình sau :
2x + 4x2 > 8
x + x2 < 5
Giải các bất phương trình sau
a) 6x2-8x+2x(2-3x)<-4 b) 2(3x+4x2)-8x(x+3)>5
a:=>6x^2-8x+4x-6x^2<-4
=>-4x<-4
=>x>1
b: =>6x+8x^2-8x^2-24x>5
=>-18x>5
=>x<-5/18
Giải các bất phương trình sau
a) 6x2-8x+2x(2-3x)<-4 b) 2(3x+4x2)-8x(x+3)>5
a)\(6x^2-8x+2x\left(2-3x\right)< -4\)
\(\Leftrightarrow6x^2-8x+4x-6x^2< -4\)
\(\Leftrightarrow-4x< -4\)
\(\Leftrightarrow-4x.\dfrac{-1}{4}>-4\cdot\dfrac{-1}{4}\)
\(\Leftrightarrow x>1\)
Vậy bất phương trình có nghiệm là \(S=\left\{xIx>1\right\}\)
b)\(2\left(3x+4x^2\right)-8x\left(x+3\right)>5\)
\(\Leftrightarrow6x+8x^2-8x^2-24x>5\)
\(\Leftrightarrow-18x>5\)
\(\Leftrightarrow-18x\cdot\dfrac{-1}{18}< 5\cdot\dfrac{-1}{18}\)
\(\Leftrightarrow x< -\dfrac{5}{18}\)
Vậy bất phương trình có nghiệm là \(S=\left\{xIx< -\dfrac{5}{18}\right\}\)
Giải các phương trình sau:
a) x − 1 2 − 2 x + 5 2 = 0 ;
b) x 2 − 1 − x 2 − 2 x − 1 2 = 0 ;
c) x 3 + 8 = − 2 x x + 2 ;
d) 4 x 2 + 8 x − 5 = 0 .
Xét dấu các biểu thức sau:
f(x)=x(16-4x2)
Giải các bất phương trình sau:
5-x/(x-3)(2x-1)<0
Giải các bất phương trình sau: 4 x 2 + 3 . 3 x + x . 3 x < 2 x 2 . 3 x + 2 x + 6
Ta có bất phương trình đã cho tương đương với
4 x 2 + 3 . 3 x + x . 3 x - 2 x 2 . 3 x - 2 x - 6 < 0
⇔ 3 + x - 2 x 2 3 x − 2(x − 2 x 2 + 3) < 0
⇔(−2 x 2 + x + 3)( 3 x − 2) < 0
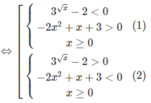
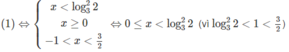
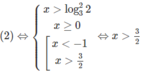
Vậy nghiệm của bất phương trình là x > 3/2 hoặc
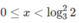
Xét dấu các biểu thức sau:
f(x)=x(16-4x2)
Giải các bất phương trình sau:
5-x/(x-3)(2x-1)<0
CHỈ GHI PHẦN KẾT LUẬN THÔI Ạ
![]()
Xét dấu các biểu thức sau:
f(x)=x(16-4x2)
Giải các bất phương trình sau:
5-x/(x-3)(2x-1)<0
CHỈ GHI PHẦN KẾT LUẬN THÔI Ạ.
Giải các bất phương trình sau:
a) 2 x − 7 > 11 − 4 x ; b) x − 2 2 − x 2 − 8 x + 3 ≥ 0 ;
c) 2 3 − 3 x − 6 2 > 1 + 3 x 6 ; d) x − 5 x + 1 + 4 x + 3 < − 5 x 2
Bài 1: Giải các phương trình dưới đây
1) x2 - 9 = (x - 3)(5x +2)
2) x3 - 1 = (x - 1)(x2 - 2x +16)
3) 4x2 (x - 1) - x + 1 = 0
4) x3 + 4x2 - 9x - 36 = 0
5) (3x + 5)2 = (x - 1)2
6) 9 (2x + 1)2 = 4 (x - 5)2
7) x2 + 2x = 15
8) x4 + 5x3 + 4x2 = 0
9) (x2 - 4) - (x - 2)(3 - 2x) = 0
10) (3x + 2)(x2 - 1) = (9x2 - 4) (x + 1)
11) (3x - 1)(x2 + 2) = (3x - 1)(7x - 10)
12) (2x2 + 1) (4x - 3) = (x - 12)(2x2 + 1)
1: \(\Leftrightarrow\left(x-3\right)\left(x+3\right)-\left(x-3\right)\left(5x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(-4x+1\right)=0\)
hay \(x\in\left\{3;\dfrac{1}{4}\right\}\)
2: \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)-\left(x-1\right)\left(x^2-2x+16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1-x^2+2x-16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x-15\right)=0\)
hay \(x\in\left\{1;5\right\}\)
3: \(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x-1\right)\left(2x+1\right)=0\)
hay \(x\in\left\{1;\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
4: \(\Leftrightarrow x^2\left(x+4\right)-9\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)\left(x+3\right)=0\)
hay \(x\in\left\{-4;3;-3\right\}\)
5: \(\Leftrightarrow\left[{}\begin{matrix}3x+5=x-1\\3x+5=1-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-6\\4x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
6: \(\Leftrightarrow\left(6x+3\right)^2-\left(2x-10\right)^2=0\)
\(\Leftrightarrow\left(6x+3-2x+10\right)\left(6x+3+2x-10\right)=0\)
\(\Leftrightarrow\left(4x+13\right)\left(8x-7\right)=0\)
hay \(x\in\left\{-\dfrac{13}{4};\dfrac{7}{8}\right\}\)
1.
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(5x-2\right)\)
\(\Leftrightarrow x+3=5x-2\)
\(\Leftrightarrow4x=5\Leftrightarrow x=\dfrac{5}{4}\)
2.
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)=\left(x-1\right)\left(x^2-2x+16\right)\)
\(\Leftrightarrow x^2+x+1=x^2-2x+16\)
\(\Leftrightarrow3x=15\Leftrightarrow x=5\)
3.
\(\Leftrightarrow4x^2\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2};x=-\dfrac{1}{2}\end{matrix}\right.\)
7.
\(\Leftrightarrow x^2+2x-15=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
8.\(\Leftrightarrow x^4+x^3+4x^3+4x^2=0\)
\(\Leftrightarrow x^3\left(x+1\right)+4x^2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^3+4x^2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=0;x=-4\end{matrix}\right.\)
9.\(\Leftrightarrow\left(x-2\right)\left(x+2\right)=\left(x-2\right)\left(3-2x\right)\)
\(\Leftrightarrow x+2=3-2x\)
\(\Leftrightarrow3x=1\Leftrightarrow x=\dfrac{1}{3}\)
Giải phương trình sau:
(2x+1)(x2-1)=4x2-2x-2
\(\Leftrightarrow2x^3-2x+x^2-1-4x^2+2x+2=0\)
\(\Leftrightarrow2x^3-3x^2+1=0\)
\(\Leftrightarrow2x^3-2x^2-x^2+1=0\)
\(\Leftrightarrow2x^2\left(x-1\right)-\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2-x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2-2x+x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(2x+1\right)=0\)
=>x=1 hoặc x=-1/2
\(\left(2x+1\right)\left(x^2-1\right)=4x^2-2x-2\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=4x^2-4x+2x-2\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=4x\left(x-1\right)+2\left(x-1\right)\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=\left(4x+2\right)\left(x-1\right)\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=2\left(2x+1\right)\left(x-1\right)\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)-2\left(2x+1\right)\left(x-1\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1-2\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)