Tam giác ABC có trọng tâm G(2;-3) và B(1;1) đường thẳng denta : x-y-4=0 đi qua A và đường phân giác trong góc A cắt BC tại I sao cho S IAB=4/5 S IAC Viết ptdt BC biết xA>0

Những câu hỏi liên quan
Cho tam giác ABC, A(4;0) B(2;-4) C(0;-2). Gọi G là trọng tâm tam giác ABC. GỌi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Chứng minh tam giác ABC, tam giác MNP có cùng trọng tâm
Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm
Đúng 2
Bình luận (0)
cho 2 tam giác đều abc và a'b'c' có chung trọng tâm g. Gọi x,y,z lần lượt là trung điểm aa',bb',cc'. CMR: tam giác xyz cũng là tam giác đều và có trọng tâm g
Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.
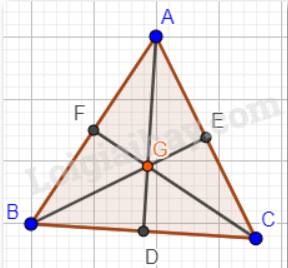
Tam giác ABC đều nên AB = AC = BC.
G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD.
Xét tam giác ADB và tam giác ADC có:
AB = AC (tam giác ABC đều);
AD chung
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)
Tương tự ta có:
\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)
\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)
Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF.
Vậy G cũng là trực tâm của tam giác ABC.
Đúng 0
Bình luận (0)
CMR : G là trọng tâm tam giác G1G2G3 trong đó G1 là trọng tâm A'BC G2 là trọng tâm AB'C G3 là trọng tâm ABC' tam giác A'B'C' và tam giác ABC có cùng trọng tâm G

Bài 1 :Cho tam giác ABC có hai đường trung tuyến BE và CF cắt nhau tại G.Chứng minh G là trọng tâm của tam giác ABC.(Gợi ý trọng tâm là điểm chung của ba đường trung tuyến nên trọng tâm là điểm chung của...)
Bài 2 Cho tam giác ABC có đường trung tuyến AD và trọng tâm G.Đã biết GA=2/3 AD,hãy chứng minh GA=2GD,AD=3GD.
Các pn giúp mk chứng minh tính chất trọng tâm của tam giác nha.
Nghĩa là: cho tam giác ABC có G là trọng tâm tam giác . Chứng minh AG = 2/3 độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác ABC.
cho tam giác abc có trọng tâm g trung điểm của ga gb gc lần lượt là m n p phép vị tâm g biến tam giác abc thành tam giác mnp có tỉ số là?
Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.
Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành
A. Tam giác GBC
B. Tam giác DEF
C. Tam giác AEF
D. Tam giác AFE
Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F ⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B
Đúng 0
Bình luận (0)
Cho tam giác ABC có A(–2; 2), B(6; –4), đỉnh C thuộc trục Ox. Tìm tọa độ trọng tâm G của tam giác ABC, biết rằng G thuộc trục Oy
A. G(0;2/3)
B. G(0;-2/3)
C. G(3; -2/3)
D. G(-3;-2/3)
* Do đỉnh C thuộc trục Ox nên C(a;0).
G thuộc trục Oy nên G(0; b).
* G là trọng tâm tam giác ABC nên:
x G = x A + x B + x C 3 y G = y A + y B + y C 3 ⇒ 0 = − 2 + 6 + a 3 b = 2 + ( − 4 ) + 0 3 ⇔ a = − 4 b = − 2 3
Tọa độ trọng tâm tam giác ABC là G 0 ; − 2 3
Đáp án B
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho tam giác ABC biết A(2;1);B(7;4);C( 6;9). Gọi G là trọng tâm ABC. 1/ Tìm tọa độ trọng tâm G của tam giác ABC. 2 Với M(–2:19). Chứng minh ba điểm A, G, M thẳng hàng.

















